11 Cost of Capital
11.1 Introduction
At the end of this chapter, you will be able to:
- explain the Weighted Average Cost of Capital (WACC) and what it measures
- calculate the cost of individual sources of capital
- calculate capital-structure weights
- calculate the WACC
- explain the relationship between CAPM and the appropriate discount rate for a project
- critically evaluate the use of WACC as the discount rate of a project.
You may have wondered a few times by now: how do we determine the discount rate for a capital budgeting project?
We have hinted in a few places that the return required on the investment of capital (i.e. the discount rate) depends on the risk of the investment.
If you start a small business the discount rate may be quite straightforward. Let's say you start a martial arts gym and you have borrowed the initial cost of $5,000 from the bank at 10% p.a., compounded annually for the life of the project (estimated at 5 years). In that case, you will need to make at least 10%, given this is your cost of capital in order to turn a profit, and as such the discount rate you should use is 10%. However, it gets complicated for larger businesses and complicated projects. In this chapter we will learn how to estimate the appropriate discount rate for a project, which is determined by the Weighted Average Cost of Capital (WACC).
11.2 The Cost of Capital – Concepts
In Chapter 10 we talked about the relationship between risk and return. Intuitively, it makes sense that a riskier investment will require a higher expected return. Consider these two alternative investments:
| Investment | A | B |
|---|---|---|
| Initial Cost | $100 | $100 |
| Payoff at the end of one year | $105 | Flip a coin - if it's heads you receive $120; if it's tails you receive $90 |
Investment A always pays $105, so it’s expected payoff is $105.
Which Investment would you prefer?
Most people would say investment A because the two investments have the same expected payoff, but investment B involves risk.
Now, what if the payoff for investment B were $125 for heads and $95 for tails? Do you want a guaranteed $105, or the expected payoff of $110 from investment B? Your answer will depend on several factors:
- How much will it hurt you if you lose the coin flip?
- What other investments do you have, and are they correlated with investment B?
- Are there any non-financial reasons to object to either A or B? For example, ethical or environmental concerns.
The first factor - how much will it hurt you to lose - is essentially measuring your level of risk aversion; how much you like or dislike risk. If two investments have the same payoff a risk averse investor will always choose the investment with the least risk.
The second factor - your other investments - considers the impact of diversification on the risk you actually face. Say you also own investment C. The cost of investment C is $100. The payoff of investment C depends on the same coin flip as investment B. If the coin lands on heads, Investment C will pay $95, but if the coin lands on tails, Investment C will pay $125. Consider the payoffs to two possible combinations of investment: A & C or B & C (all owned in equal amounts):
| Coin Flip | A&C | B&C | 2A |
|---|---|---|---|
| Heads | $105 + $95 = $200 | $125 + $95 = $220 | $105 × 2 = $210 |
| Tails | $105 + $125 = $230 | $95 + $125 = $220 | $105 × 2 = $210 |
Because B and C move in opposite directions, owning them together actually reduces your risk relative to owning either on it’s own. Furthermore, since B and C both have a higher expected payoff than A, owning B and C together provides a higher return than investing in two units of A.
From this example, we can see that more risk requires a higher return, but not all risk is the same. In Chapter 10 we learned that there’s systematic risk and unsystematic risk. We don’t get compensated for unsystematic risk because we can eliminate it by diversifying. The lesson from all of this is that the appropriate return for a given investment depends only on its level of systematic risk - how highly correlated is the investment with all of the other investments in the economy? Furthermore, if we can find two investments with the same level of systematic risk, those two investments will have the same expected return.
How do we determine the appropriate level of risk for a project or investment? There are two main ways:
1) Measure its systematic risk (beta) OR
2) Find another investment with the same systematic risk.
Fortunately, the second approach is often fairly easy. If a company has a single line of business, then whatever return is required on that company’s assets is the same as the return required to expand their operations in the same area. For example, if Myer Holdings Ltd (ASX code MYR) wanted to open a new Myer store, then the required return for that store will be the same as the required return on Myer's existing assets since the company owns only the one line of business. However, if Myer wanted to expand into the mining business, they would not be able to use this return. In this case they would have to estimate the systematic risk from the operations of a business that is already in the mining business, for example BHP.
How do we know what return is required on a company’s assets?
Think about how you might buy a company’s assets - you could buy the assets directly, or you could buy all of the debt and all of the equity in the company. After all, the company has purchased their assets using the debt (money they have borrowed) and equity (money owners have invested) that is on their balance sheets. This means that a portfolio of the debt and equity of a company must have the same expected return as the assets of that company: they are just two ways of buying the same investment. So, if we want to measure the expected return for a company’s assets, we just compute the weighted average of the return on the company’s debt and equity. This is known as the Weighted Average Cost of Capital or WACC.
Required Return is the return that the firm must earn to compensate investors for the capital they provide to finance projects. In other words, the required return is the return required to attract capital - that’s why required return and cost of capital are just two names for the same concept.
Note: the cost of capital depends on the use of the funds, not the source. Whether we use debt or equity to finance the project doesn’t matter and does not affect our decision to go ahead with the project or not.
Knowledge Check
AlphaBeta Ltd is evaluating the purchase of commercial real estate. Which of these factors will affect the required return?
11.3 Weighted Average Cost of Capital (WACC)
A firm’s assets are financed by a combination of long-term liabilities (debt) and shares (equity). Buying all of the debt and all of the equity of a firm is equivalent to buying all of the assets of the firm.
Remember the accounting identity: Assets = Liabilities + Equity.
The capital that finances the firm is a portfolio of the debt and equity of the firm. Therefore, the cost of capital is the weighted average of the return required on these two sources of capital. We have learnt how to compute the return on a portfolio - it’s simply the weighted average of the returns on the investments in that portfolio, where the weights are based on market values. Therefore, a weighted average of the firm’s cost of debt and equity will measure the required return for the firm’s assets:
[latex]W A C C=\frac{E}{V} \times E\left(R_{e q u i t y}\right)+\frac{D}{V} \times E\left(R_{d e b t}\right) \times(1-\text {taxrate})[/latex]
Where [latex]R_{e}[/latex] is the expected return on equity, [latex]R_{d}[/latex] the expected return on debt. There are a few things to note about this equation. First, the weights are computed based on market values. [latex]E[/latex] is the market value of all of the shares and [latex]D[/latex] is the market value of all of the debt.
[latex]V=D+E[/latex]
Second, the debt term is multiplied by [latex](1-\text { tax-rate})[/latex]. This is because the corporate tax rules treat debt different to equity. When a company pays interest on debt, they are allowed to deduct that interest from their taxable income. That means that $100 of interest expense only costs the firm 100 [latex]\times(1-\text { tax-rate})[/latex] or $70 at a 30% tax rate. To account for this, we measure the cost of debt on an after-tax basis.
To measure WACC we need:
- Cost of equity [latex]R_{e}[/latex] which is the required return on shares.
- Cost of debt [latex]R_{d}[/latex] which is the market yield on the firm’s debt.
- Market value of debt and equity to compute the weights.
11.4 Estimating Returns
11.4.1 Cost of Equity
The cost of equity is hard to observe. There are two methods we can use to estimate [latex]E\left(R_{e q u i t y}\right)[/latex]: the dividend growth model and the Capital Asset Pricing Model (CAPM). To use the dividend growth model, we assume constant dividend growth and estimate the growth rate using historical dividend growth rates or analyst forecasts. Remember that the dividend growth model is [latex]P_{0}=\frac{D_{1}}{r-g}[/latex]. We can rearrange this to get [latex]r=\frac{D_{1}}{P_{0}}+g[/latex], which is what we need.
Let’s apply this to some real numbers:
AGL Energy Ltd (AGL) is an Australian energy provider, that both produce energy (electricity, gas, solar) and provides retail distribution. Over the last ten years AGL has paid the following dividends:
| Year | Dividend | Growth |
|---|---|---|
| 2009 | 0.54 | |
| 2010 | 0.59 | 9.26% |
| 2011 | 0.6 | 1.69% |
| 2012 | 0.61 | 1.67% |
| 2013 | 0.63 | 3.28% |
| 2014 | 0.63 | 0.00% |
| 2015 | 0.64 | 1.59% |
| 2016 | 0.68 | 6.25% |
| 2017 | 0.91 | 33.82% |
| 2018 | 1.17 | 28.57% |
| 2019 | 1.19 | 1.71% |
Averaging ten years of growth rates, we get an average annual growth rate of 8.78%. The current share price of AGL is $19.66. If we assume that the 8.78% average growth rate will continue indefinitely, we can estimate the required return on equity for AGL:
[latex]E\left(R_{e q u i t y}\right)=\frac{1.19 \times 1.0878}{19.66}+0.0878=0.1536[/latex] or [latex]15.36 \%[/latex]
(Why do we have to multiply the 2019 dividend by 1.0878? Because the formula needs next year’s dividend - so we have to estimate the 2020 dividend. Since we’re assuming that dividends grow at 8.78%, the 2020 dividend will be [latex]1.19 \times 1.0878 = 1.29[/latex])
Does this look realistic to you? 8.78% is a fairly high growth rate to be applying to a perpetuity. If we remove the two outliers (2017 and 2018 with >20% growth), the average growth rate becomes 3.18%, which is much more reasonable. At 3.18% growth,
[latex]E\left(R_{e q u i t y}\right)=\frac{1.19 \times 1.0318}{19.66}+ 0.0318=0.0943[/latex] or [latex]9.43 \%[/latex]
The advantage of using this method to estimate the required return on equity is that it is fairly straightforward and the data is easy to obtain. However, this only works for companies that pay dividends, and the required return is very sensitive to the estimated growth rate. Additionally, we have not explicitly considered the riskiness of the return or the uncertainty of our forecasts.
The other method of estimating the required return on equity is to use the Capital Asset Pricing Model (CAPM). Recall equation 12 from Chapter 10:
[latex]E[r]=r_{f}+\beta\left(E\left[r_{m}\right]-r_{f}\right)[/latex]
This equation tells us that the expected return on any asset (including equities) is a function of the risk free rate, beta, and the expected return on the market portfolio (a portfolio of all assets available for investment).
Risk Free Rate: The appropriate risk free rate is the yield on a government bond that matches our expected investment horizon - this is often approximated with a 10-year government bond, which is currently around 1.1%.
Expected return on the market portfolio: This can be approximated by the average total return on the ASX - which has historically been around 8%.
Beta: Beta is computed using a linear regression on historical prices. For listed companies, you can often find beta on Yahoo Finance or similar services. At the time the data for this example was gathered, AGL had a beta of 0.90.
Applying these numbers to the CAPM equation, we can estimate the expected return on AGL shares as:
[latex]R_{e q u i t y}=E[r]=r_{f}+\beta\left(E\left[r_{m}\right]-r_{f}\right)=0.011+0.9 \times(0.08-0.011)[/latex]
[latex]=0.0731[/latex] [latex]{ or }[/latex] [latex]7.31 \%[/latex]
Since we’re using CAPM to estimate the return on AGL shares, the resulting return is AGL’s return on equity.
The advantages of using this method to estimate the required return on equity are that we are explicitly adjusting for risk and this method doesn’t require steady dividend growth (or, indeed, any dividends at all). The CAPM method applies to projects, equity, and anything we can compute or estimate beta for.
However, we must estimate the expected return on the market, risk-free rate, and beta. In practice, this often means that we are relying on past data to predict the future.
11.4.2 Cost of Debt
The cost of debt is the return lenders require on new debt. The purpose of computing WACC is to determine the current required return for a company’s assets - so we need to look at current market values and current interest rates or returns.
For bank loans, we should be looking at current bank interest rates.
For bonds, we should be looking at the current market yield for traded bonds.
If these rates are not easily available, then we can approximate the appropriate rate by looking at bonds of companies with similar credit ratings. Be sure to express any bond yield as an annually compounded interest rate (see Chapter 3 section 5 where we discussed the computation of Effective Annual Rates).
Exercises
Knowledge Check
You are computing the WACC for Barty Ltd. You have the following pieces of information:
- Barty Ltd. shares are traded on the ASX. You have estimated that the beta of Barty Ltd. shares is 1.3
- Assume that the risk free interest rate is 1.0% and the market risk premium is 7%.
- Barty Ltd is funded partially by debt in the form of bonds.
- Barty Ltd bonds have a coupon rate of 5%, pay annual coupons, and have 10 years remaining until maturity.
- Barty Ltd bonds have a BBB credit rating, but are not publicly traded.
Your research has shown that BBB bonds with the same maturity date as Barty Ltd bonds are currently being issued at a market yield of 4.5% p.a. with annual coupons.
Which of the following represents the best estimates of the cost of debt and equity for Barty Ltd.?
11.4.3 Market Values
To compute WACC, we also need the weights. Remember,
[latex]W A C C=\frac{E}{V} R_{e}+\frac{D}{V} R_{d}(1-t)[/latex]
Computing E, D and V is fairly straight forward. We’re computing WACC to measure what investors currently require as a return on the assets of the company. Since we want a current value, we need to use market values and current returns in the equation.
So, E is just the current market value of equity. This is also known as the “market capitalisation” and is computed as the current share price times the number of shares on issue. For public companies, market capitalisation is commonly reported. Take a look at Yahoo Finance and see if you can find the current market capitalisation of AGL (often abbreviated as “Market Cap”). In November 2019, AGL had a market capitalisation of around A$13 billion. WACC is often computed using the most recent financial statements - analysts can easily look up the share price and multiply by the number of shares on issue, as reported in the annual report.
D is computed as the current market value of debt. Many companies have both public and private debt, meaning it is not easy to compute the current market value of their debt. If all debt is in the form of bonds, then we can use the bond valuation formula and current market yield to compute market value. Most companies, however, have a combination of bank debt, public bonds, and private debt, and analysts outside of the company often do not have sufficient information to compute current market value. In this case, analysts tend to assume that the book value of debt (the original value) is a reasonable estimate of the market value of debt.
Once we have E and D, we have V as: [latex]V=E+D[/latex]
Do you think it is reasonable to use book value as an estimate of market value for debt? Why or why not?
11.4.5 Putting it all Together
So, now we have all of the pieces we need to compute WACC:
-
-
- Cost of equity: [latex]R_{\text e}[/latex]
- Cost of debt: [latex]R_{\text d}[/latex]
- Market value of equity: [latex]E[/latex]
- Market value of debt: [latex]D[/latex]
- Market value of assets: [latex]V=E+D[/latex]
-
The final variable is the corporate tax rate. For large Australian firms, this will be 30%.
As a share analyst, you have found the following facts about Pineapple Ltd:
-
-
- Market capitalisation is $650 million
- Beta of Pineapple shares is 1.3
- The risk free rate is 4%
- The expected return on the market portfolio is 9.5%
- Pineapple has $250 million in bank loans which have a variable interest rate that is currently 4.5% compounded annually
- Pineapple faces a 30% corporate tax rate
-
What is WACC for Pineapple Ltd?
[latex]E=\$ 650 \text { million (market cap) }[/latex]
[latex]D=\$ 250 \text { million (estimate with book value) }[/latex]
[latex]V=E+D=\$ 900 \text { million }[/latex]
[latex]E\left(R_{\text {equity}}\right)=4 \%+1.3(9.5 \%-4 \%)=11.15 \%[/latex]
[latex]E\left(R_{d e b t}\right)=4.5 \%[/latex](current bank rate)
[latex]W A C C=\frac{650}{900} \times 11.15 \%+\frac{250}{900} \times 4.5 \% \times(1-0.3)=8.93 \%[/latex]
Exercise
Kumquat Ltd has asked for your assistance in computing WACC. Looking through the financial records they have provided, you find the following facts:
- Kumquat Ltd is not publicly traded, so a current share price must be estimated.
- Kumquat has 50,000 shares on issue
- Last year Kumquat paid dividends of $10.50 per share. Dividend policy is to increase the cash dividend by 3% per year indefinitely (you can assume that income projections and budgets support this policy)
- Based on Kumquat’s business and capital structure, beta for Kumquat shares is estimated at 1.5.
- The current risk free interest rate is 2% and the expected return on the market portfolio is 8%.
- Kumquat’s only debt is a private bond issue. A total of 2,000 bonds were issued with a face value of $1,000 per bond. The bonds pay annual coupons of 6%. Based on current market conditions, Kumquat’s CFO estimates that the market yield for Kumquat bonds is 4%. These bonds have ten years remaining until maturity.
- Kumquat faces a corporate tax rate of 30%.
What is the WACC of the company?
VIDEO: Worked example: WACC Kumquat (YouTube, 21m22s)
11.6 WACC and the Discount Rate for NPV
When computing WACC, we are using current market values and current market interest rates. Essentially, we’re computing the expected return on a portfolio that consists of all of the firm’s debt and all of the firm’s equity. If we were to purchase all of the debt and equity of a firm, what would that entitle us to? What we would get is the net cash flows (incoming cash flows minus outgoing cash flows) from all of the firm’s assets - because that’s what firms use to pay interest and dividends to investors. And, if we own all of the firm’s capital, we then control how the firm uses its assets - purchasing all the debt and equity should be equivalent to purchasing the firm’s assets directly.
Therefore, WACC is measuring the return the market requires for the assets of the company. If a company’s assets are all pretty much the same, then we can use WACC as an estimate of the required return on projects in the same line of business as the rest of the company. However, if a company has a variety of business lines, what WACC is measuring is the return on that portfolio of assets or businesses - not the return on any single asset or line of business.
From Chapter 10 we know that the required return depends on systematic risk. So, if WACC measures the return required on assets, it’s also measuring the required return for any investment with the same systematic risk (beta) as the assets of the firm. When we determine the required return for a project (e.g. for computing NPV), what matters is the systematic risk of that project. Therefore, we can use WACC as the required return for NPV if (and only if) the systematic risk of the project we’re evaluating is the same as the average systematic risk of the firm’s assets. When is this likely to be true?
Finally, note that the required return for a project depends on the systematic risk of the project, not the risk (or average return, or WACC) of the company.
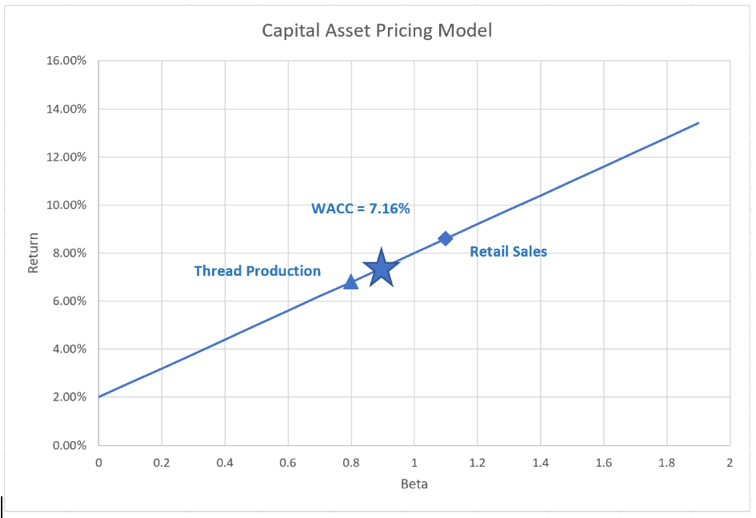
When a company has only one line of business, then WACC is useful for determining the required return for projects in that line of business. Where a company has multiple lines of business, another approach must be taken. There are two common ways that conglomerate companies address this issue:
Pure Play Approach: Try to find companies that focus exclusively on the type of project we are valuing and use WACC from these companies as the cost of capital for our project.
Subjective Approach: Divide projects/divisions/ business lines into risk categories and apply a subjective adjustment to WACC for each category. Low systematic risk projects might be required to return 2% less than WACC and high systematic risk projects might be required to return 2% more than WACC.
Exercise
Mark each statement as either “appropriate” or “not appropriate".
11.7 Summary and Key Formulas
11.7.1 Summary
Up until now, when doing capital budgeting questions, you have always been given the discount rate to use. This chapter taught you how to calculate that discount rate for yourself. The rate at which we discount cash flows is the required return for the project, which is the cost of capital for the firm, or the weighted average cost of capital (WACC).
When calculating WACC you need information on the sources of capital, meaning how much of your capital comes from borrowing money (debt) and how much comes from investors (equity).
- E stands for the amount of equity a company has. We can calculate this by multiplying the share price by the number of shares.
- D stands for the amount of debt a company has. We can find this by calculating the present value of all the debt (normally bonds) the company has issued.
- After we have calculated the amounts of E and D we have we then need to calculate the cost of these sources of capital.
- When it comes to the cost of equity, [latex]R_e[/latex], there are two ways that it can be calculated. If you are given information about a recent dividend and the dividend growth rate you can use the dividend discount model to do your calculation. If you are given information about the beta (systematic risk) of a company as well as the risk-free rate and expected return on the market (or market risk premium), you can use CAPM to calculate [latex]R_e[/latex].
- [latex]R_d[/latex] is the market yield on the bonds the company has on issue. If they have more than one type of bond on issue you need to calculate the weighted average of the different yields.
After you have collected all of this information, as well as the tax rate, you can go ahead and calculate WACC.
You have to be able to decide if a particular WACC is appropriate for a project. For example, if a company is thinking about expanding into an area of business that is different from what it currently does, its current WACC would not be an appropriate discount rate. The two major ways of dealing with this problem are the Pure Play Approach and the Subjective Approach.