3 Time Value of Money (Part 1)
3.1 Introduction
At the end of this chapter, you will be able to:
- visualise cash flows using timelines
- explain the concept of time value of money
- apply time value computations to present and future values
- explain how compounding applies to non-financial contexts
- calculate comparable interest rates regardless of how they are quoted.
Click the accordion to access the text of the video (you can skip this if you watched the video)
3.2 Timelines
We can make our lives much easier by visualising the concept of time value of money using timelines. A timeline allows you to visually present cash flows, most importantly, the timing of the cash flows as well as their nature as either inflows or outflows. This helps you better understand an investment project, an event, or any other forms of financial transactions.
3.2.1 Timelines Introduction
NOTE!
We adopt the following conventions in setting up timelines:
- Cash flows occur at the end of each time period (unless otherwise stated)
- Cash outflows are entered as negative (-ve) values
- Cash inflows are entered as positive (+ve) values
- The start of the time period we are evaluating is represented by n = 0
Exercise
Concept check: Part A
Michael is investing $15,000 in a 5-year bank term deposit that pays a 6% annual interest ($900) at the end of each year. After five years, Michael will receive his $15,000 back.
Which of these timelines correctly represents the resulting cash flows from Michael's perspective?
A.

B.

C.

D.

Concept check: Part B
Your brother has asked you for a $10,000 loan and promised to pay back over a 5 year period. He has agreed to pay $1,500 at the end of the first year, $1,850 at the end of the second year, $2,500 at the end of the third year, $3,000 at the end of the fourth year, and $1,150 at the end of the fifth year.
Which of these timelines correctly represents the resulting cash flows from your perspective?
A

B

C

D

3.2.2 Comparing Cash Flows
3.2.2.1 The Basic Concept
Let’s have a look at a simple example. Assuming you can earn interest of 5% per annum in a bank savings account, let’s compare:
(A) receiving payment of $100 today
(B) receiving a payment of $100 next year.
Which option is better?
3.2.2.2 Comparing Cash Flows
Whichever computation you use, Option A, receiving $100 today is always worth more! The key to this answer is that if you were to receive $100 today, you could earn 5% interest on that sum for one year. If the interest rate were higher, the difference between the value of Option A and Option B would be even greater!
Based on this example, we can make several generalizations:
- The value of a dollar invested at a positive interest rate grows over time. Thus, the further in the future you receive a dollar, the less it is worth today.
- The trade-off between money today and money at some future date depends in part on the rate of interest you can earn by investing. The higher the rate of interest, the more likely you will elect to invest your funds (assuming no additional risk of this higher interest rate).
Note that especially when we have multiple cash flows (Chapter 4) it will be important to draw a timeline. The video below explains this in more detail.
VIDEO: Tips for Time travel (YouTube, 2m15s)
3.3 Time Value of Money Basics
3.3.1 Definitions and Mechanics of Time Value Calculations
With the use of a timeline, you should be able to correctly identify cash flows, and their respective timing, and do some simple calculations by compounding or discounting cash flows. To do simplify our calculations, it would be handy to name the five variables involved in every time value of money problem.
Video: Time Value of Money – Definitions
3.3.1.1 Time Value of Money – Definitions
- Present value (PV) - While present value can refer to the value today of a cash flow in the future, it can be helpful to think of present and future as relative terms. Whenever we are moving a cash flow backwards in time we will be using present value (discounting) computations. So, computing the value in 2025 of a cash flow promised in 2030 is a present value computation; it tells us what we will be willing to pay in 2025 for the promised cash flow in 2030.
- Future value (FV) - Value of a cash flow at some specific future time - it is the money you have in your hand at a point in time in the future. Again, future is a relative term. Whenever we are moving a cash flow forwards in time we will be using future value (compounding) computations. So, computing the value in 1990 of a cash flow we expected to receive in 1985 is a future value computation; it tells us what that cash invested in 1985 was worth in 1990.
- The number of periods (n) - This is the number of compounding periods (interest computation periods) during the investment. It is usually measured in years, but it could be any scale of time such as quarterly, monthly, or even daily.
- Interest rate (r) - This is the growth rate of your money over the lifetime of the investment. This is also called the rate of return, discount rate, interest rate or growth per period.
- Cash flows (CF) - These are a series of either single, equal, or mixed, evenly-spaced or irregular cash flows. Cash flows can be positive or negative. If we're receiving money (cash inflows) we use positive numbers, if we're paying money (cash outflows) we use negative numbers. As every investment has two sides (borrower/lender; company/shareholder; bank/depositor), each side will be looking at a mirror image of what the other side sees.
The variables are illustrated for the example we saw previously of $100 received today, earning 5% per annum, and solving for the value at year 1.
3.3.1.2 Future Value (FV)
Future Value and Compounding
Future Value (FV) of an investment is what the investment will be worth after earning interest for one or more time periods. The process of converting the initial amount into a future value is called compounding.
NOTE: If you were to invest a certain dollar amount today, it would grow to a larger (hopefully!) value at some point in the future. The value at a future point in time is called the future value. In order to calculate the future value, we must know the principal amount of investment, the rate at which the investment will grow, and the length of time that the investment will be held.
- Present value = Principal amount of investment in this problem is the $100 that is invested today.
- Rate at which the investment will grow is referring to interest rate (r) of 10% per annum.
- Length of time that the investment will be held is referring to the number of periods (n), usually measured in years.
VIDEO: Future Value Formula (YouTube, 4m17s)
The video has derived the Future Value formula as follows:
Where:
- PV is how much you have at the start of the time period you are evaluating
- r equals the interest rate you are earning on the investment
- n equals the number of periods you are putting the money away
- FV equals how much you have at the end of the period you are evaluating, the future value
- The term (1+r)n is the future value interest factor, often also known as the future value factor.
Examples
Single-period investment
Suppose you place $100 in a bank savings account that pays interest at 10% per year, and expect to hold the investment for one year. How much will the investment be worth at the end of this period? In other words, what is the future value?
Step 1) Draw a timeline

Step 2) Identify the variables you have and need
PV = $100
r = 0.10 (When doing any time value of money calculations, always express interest rate in decimal format)
n= 1
FV= ?
Step 3) Calculate your unknown variable
Thus, you would have $110 dollars in 1 year time.
Concept Check
Two-period investment
Now, suppose that at the end of the first period, you decide to hold the investment for another year. At that point, your principal (present value) will be $110 and it will grow for another year at 10%. How much money would you have at the end of the second year? (Input the number without the dollar sign )
Think about this...
From the previous example we see that $100 invested at 10% per year for 2 years will grow to $121. Notice that in the second year, you earned $11 in interest as compared to only $10 in the first tear. Where did the extra $1 come from?
That is the interest that you earned on the $10 interest from year 1 ($10 × 0.10 = $1). In other words, the extra interest came from the process of compounding!
NOTE: a two-period investment is simply two single-period investments back-to-back. After the first period, interest accrues on the original investment (principal) and on the interest earned in preceding periods. The future value of $121 at the end of year 2 consists of three parts:
The initial investment of $100.
The $20 ($10 + $10) of simple interest earned at 10% for the first and second years.
The $1 interest earned during the second year on the $10 of interest from the first year ($10 × $0.10 = $1). This is called interest on interest. The total amount of interest earned is $21 ($10 + $11), which is called compound interest.
The Power of Compound Interest
The concept that interest compounds - that is, that you earn interest on the interest earned in previous periods - is very powerful. To see the effect of compounding, compare the compound interest to the amount of interest you would earn without compounding. We call interest computed without compounding “simple interest”, and it’s computed as the interest rate times the original principal. For one period it’s the same as compound interest:
But for subsequent periods it’s quite different:
and
Exercises
Anna received a $6000 inheritance from her great Aunt at the start of 2005, which she deposited immediately. She now wants to use it for her wedding, taking place at the start of 2022. If her bank pays 3% interest per year, how much will she have for her wedding?
3.3.2 Re-arranging the FV formula
In the previous sections, you learned everything that you need to know in order to solve time value of money problems. That is quite a bold statement, but it is true! The key is that we derived basic time value of money formula to solve for future value:
[latex]FV_n=PV×(1+r)^n[/latex]
From this formula, we can easily derive other formulas for solving for any of the variables in a time value problem:
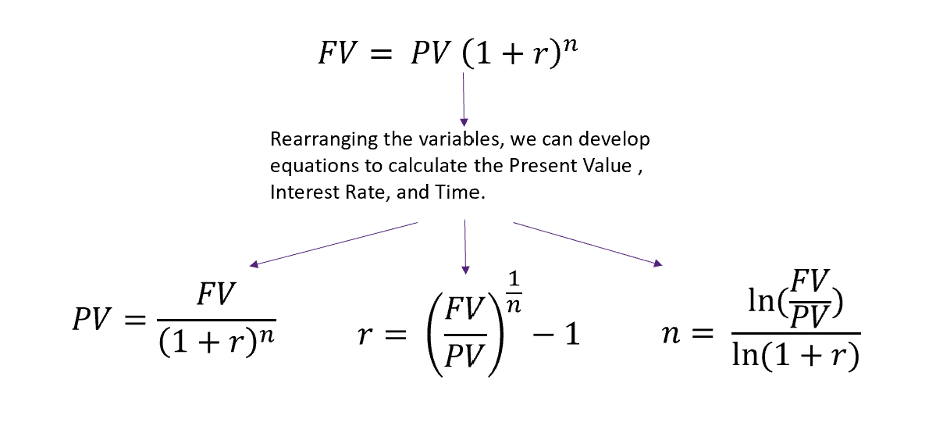
Note that the mathematical re-arranging is the “easy” part, the more difficult part is to figure out from a problem which variable you need to solve for. But don’t worry, your timelines and practice will help you!
3.3.3 Present Value (PV)
Present Value and Discounting
When calculating the Present Value (PV) of an investment, we calculate the value of a cash flow at an earlier point in time. This can be useful to understand for many reason, such as how much you need to save to achieve a desired outcome in the future.
In the video below we demonstrate an example for the following present value problem: After finishing his apprenticeship, Joe wants his own food truck. He has 2 years to save $1800 for the deposit. He knows his bank pays 6% interest, but how much does he need to deposit now to have $1800 in 2 years’ time?
VIDEO: Present Value Formula (YouTube, 2m26s)
The process of converting the future cash flows into present value is called discounting. The present value formula is:
[latex]PV=\frac{{\rm FV}_n}{\left(1+r\right)^n}[/latex]
Remember that n is the number of periods in the future that the future cash flow is located (relative to the present value). Note that as we are dividing the future value, the present value will always be less than the future value (at a positive interest rate). Accordingly, the present value can be thought of as the current value of a future cash flow that has been discounted at the appropriate discount rate.
Just as we have a future value factor (1+r), we also have a present value factor, which is more commonly known as the discount factor. The discount factor, which is [latex]\frac{\mathrm{1}}{(1+r)}[/latex] is the reciprocal of the future value factor. This expression may not be obvious in the equation above, but note that we can write that equation in two ways:
[latex]PV=\frac{{\rm FV}_n}{\left(1+r\right)^n}[/latex]
[latex]PV={\mathrm{FV}}_n\times\frac{1}{\left(1+r\right)^n}[/latex]
Example
Two-period investment - Example
Suppose your mother gives you a 10% term deposit. The term deposit matures in two years and pays $121 at maturity. The term deposit cannot be redeemed until maturity. Being a student, you want the money now and would like to sell the term deposit. What would be the fair price if you sell the term deposit today?
Step 1) Draw a timeline
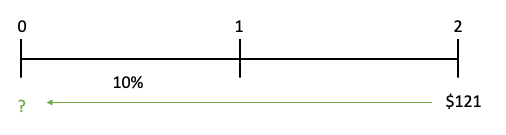
Step 2) Identify the variables you have and need
FV = $121
r = 0.10
n= 2
FV= ?
Step 3) Calculate your unknown variable
[latex]PV={\mathrm{FV}}_n\times\frac{1}{\left(1+r\right)^n}[/latex]
[latex]PV=\frac{\mathrm{$121}}{\left(1+0.10\right)^2}[/latex]
Thus, a fair price would be $100. This is because if you sell it for $100, the other party will receive a 10% return each year on this investment.
Test Your Knowledge…
Xiao is a student at UQ and is very excited about the newest Tesla car. Unfortunately, she is a student and cannot afford to buy one. She estimates that a second-hand Tesla will cost $20,000 in 6 years’ time. Her parents say that they will make a deposit now into an account earning 4% per year, which she will receive in 6 years if she graduates. How much do her parents have to deposit so that she can buy the Tesla in 6 years?
3.3.4 Interest Rate (r)
There are times where we know the cash flows that occur at different points in time, and would like to know what the interest is that is earned on the investment. For this, we would need to use our re-arranged FV formula for r:
Take the previous example where you received a term deposit from your mum. Let's say you didn't know the interest rate of this deposit, but you know that if you would currently sell it you receive $100 (the present value), whilst the value in two years would be $121, what would be the interest rate you earn if you held this investment for two year? Intuitively you may say 10%, but as calculations become more tricky it would be handy toknow the formula that can give you an answer every time.
Using the formula above, we see that a term deposit with a future value of $110, a present value of $100, and 1-year time period, gives a discount rate of 10%:
[latex]r=\left(\frac{121}{100}\right)^\frac{1}{2}-1[/latex]
[latex]r=0.1\ or\ 10\%[/latex]
Example
Calculating returns
Your great grandfather bought a share in a company for $1.20 in 1955, and this share currently sells in the market for $84.50. If he sells his share now, what is the return he earned on this investment?
Note: When asked about calculating a return, we often refer to the interest rate.
Step 1) Draw a timeline
In this question, we have the following timeline
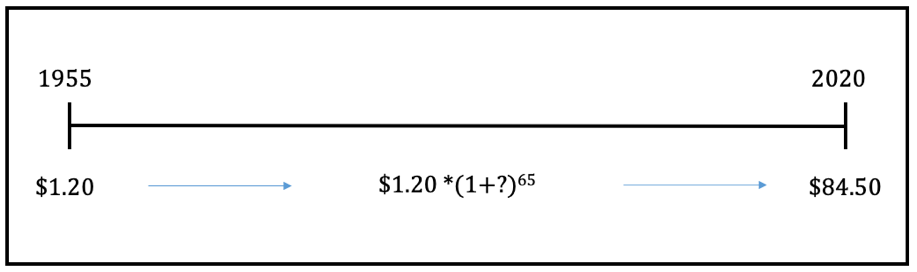
Step 2) Identify the variables you have and need
PV = $1.20
N=65 (2020-1955)
FV= $84.50
r=?
Step 3) Solve for your unknown variables
[latex]r=\left(\frac{{FV}_n}{PV}\right)^\frac{1}{n}-1[/latex]
[latex]r=\left(\frac{$84.50}{$1.20}\right)^\frac{1}{65}-1[/latex]
[latex]r=0.0676\ or\ 6.76\%[/latex]
Thus, your great grandfather made an annual return of 6.76% on his investment
Exercise
UQ has an iLab program, which helps UQ entrepreneurs (students and staff) put their business ideas into reality. During the program, several investors offer financing to the businesses. One investor offers the following, “I will invest $200,000 into your business, if you pay me $1,000,000 back in 3 years.”. What is the annual return on investment this investor asks for?
3.3.5 Number of periods (n)
Being able to calculate the number of periods can come in useful if you, for example, want to know how long it would take to save for a holiday if your money is sitting in the bank.
Again, for the term deposit example, you may say answering the following would be easy: if a term deposit pays 10% p.a., costs $100 now, and pays $110 at maturity, how many years until the term deposit matures? The answer is quite straightforward after going through the example a few times now: it would be one year. The formula we re-arranged for n however is useful when problems become more complex (which they almost always are!).
Example
Solving for n
Imagine Paul just received a gift of $2000 from his great Aunt. He would like to use this to go on a holiday after he graduates, and estimates will cost $2500. Earning 3.5% interest p.a., how long will it take until Paul has enough money for his holiday?
Step 1) Draw a timeline
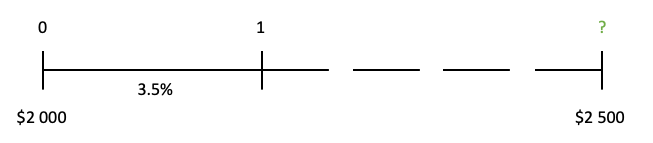
Step 2) Identify the variables you have and need
[latex]PV=2000[/latex]
[latex]FV=2500[/latex]
[latex]r=3.5%=0.035[/latex]
[latex]n=?[/latex]
Step 3) Solve for your unknown variable
[latex]n=\frac{ln\left(\frac{FV_n}{PV}\right)}{ln(1+r)}[/latex]
[latex]n=\frac{ln\left(\frac{2500}{2000}\right)}{\ln{\left(1+0.035\right)}}=6.4864\ years[/latex]
If Paul plans to graduate in about 4 years, he will not have enough for his holiday from his Aunt's funds alone.
Test Your Knowledge…
Adriana just turned 22 and just received a big pay-out from her job. She decides to make an extra contribution of $1000 towards her superannuation. She hopes that when she retires, she can use it to hire someone to build a nice garden for her, estimating to cost $10,000. If her superannuation fund pays a return of 5.5% p.a., how old will she be when she has enough for her garden?
3.3.6 Using Excel
In Excel, the variables we have used so far are named as follows:
- PV = PV (so, the same!)
- FV = FV (so, the same!)
- r = rate
- n = nper
When solving for e.g. PV, you simply type "=PV(" and it will automatically guide you through the process:
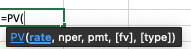
You can follow the same process for solving for n: "=nper(...)" etc.
You also see a variable "pmt" and "[type]". With a single cash flow, which is what we worked with in this chapter, you should leave the variable "pmt" at zero. You will learn in Chapter 4 when we can use the "pmt" function/variable. You can close the bracket after filling out your FV, as we use the default function for "[type]".
Exercise
1. What is the difference between compounding and discounting?
2. You are planning to invest $30,000 today in an investment fund that will provide a return of 11% each year. What will be the value of the investment in 10 years?

3. Your sister has asked you for a loan and has promised to pay back $15,000 at the end of 3 years. If you normally invest to earn 6% per annum, how much will you be willing to lend to your sister?

4. Simon decided to invest in his favourite stock Tesla on 30 December 2016, when the share price was 42.73USD. Exactly 4 years later, the stock price was 694.78 USD. If Simon sold his share after 4 years, what would be the annual return he earned?
5. Your uncle bought his home for $85 000 a long time ago. Its current value is $500 000 (assume January 2020). He says to you "Buying my house was a great investment, so far I've made a return of 8% p.a." Assuming yearly compounding, in what year did your uncle buy the house?
3.4 Compounding in Non-Financial Settings
The concept of compounding is not restricted to money. Any number that grows over time, such as the population of a city or the number of frogs in a pond, could grow at some compound growth rate. Compound growth occurs when the initial value of a number increases or decreases each period by a factor (1+ growth rate). As we go through the course, we will discuss many different types of interest rates, such as the discount rate on capital budgeting projects, the yield on a bond and the internal rate of return on an investment. All of these “interest rates” can be thought of as a growth rate (g) that relates future values to present values.
When we refer to the compounding effect, we are really talking about what happens when the value of a number increases or decreases by [latex]\left(1+growthrate\right)^n[/latex]. Does this sound familiar? If we want, we can rewrite the future value equation in a more general form as a compound growth rate formula, substituting g, the growth rate, for r, the interest rate.
Where:
Future value of the economic factor, such as sales or population, at the end of period n.
PV = Original amount or present value of economic factor
g = Growth rate per period
n = Number of periods; a period may be a year but can also be a quarter, month, week, day, minute, or any other length of time.
How do we apply this equation in a non-financial setting?
The world’s population in 2017 is therefore estimated to be:
The following graph shows how different world regions have grown since 1820.
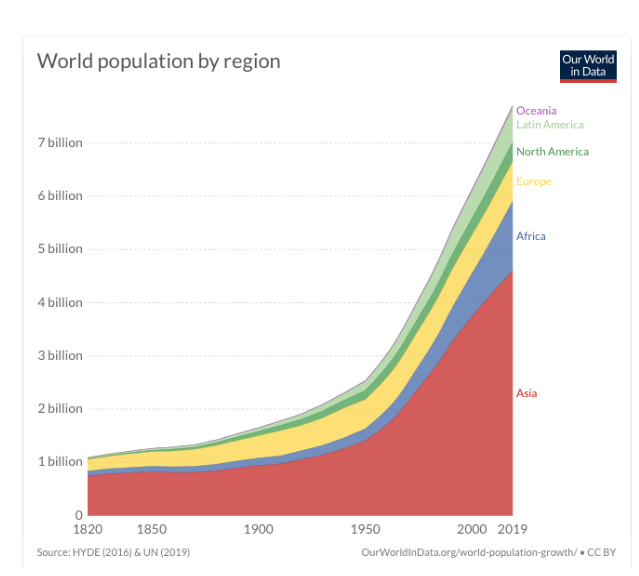
Since the 1950's the world has seen unprecedented and exponential growths in population and wealth, which have gone paired with numerous socio-economic changes such as energy use and fertiliser consumption for food production. These changes have made our lives a lot better and more comfortable. In turn, these anthropogenic (=human caused) changes are affecting our earth system in unprecedented ways, such as increasing the concentration of greenhouse gases in the atmosphere and the altering of land from forests to farms or domesticated land, causing a loss of biodiversity on a global scale.
Read this article on Acceleration by the International Geosphere Biosphere Program. This will show you the implications of exponential growth in population and the increase in GDP.
For additional materials on the topic, you can view the following video on The Exponential Function where, decades ago, physics professor Albert Bartlett argued that "The greatest shortcoming of the human race is our inability to understand the exponential function"
VIDEO: Dr. Albert Bartlett: Greatest Shortcoming of Human Race and the Exponential Function (YouTube, 2m4s)
3.5 Interest Rates: Compounding Period and Interest Rate
Each of the time value formulas contains an interest rate, r, and a number of time periods or payments, n. For each problem or investment, interest is compounded at a given frequency - this could be annual, quarterly, monthly, etc. Compounding frequency depends on the facts given. If you borrow money from a bank, the contract will state how frequently interest will be compounded. We care about compounding frequencies for 2 main reasons:
- Interest rate, r, have to match with the frequency of the payments n.
- Interest rates with different compounding periods cannot be compared (next section)
The problems we’ve dealt with so far have all involved annual compounding. In that case, the compounding period is a year, and the appropriate interest rate is the annual rate itself. Things are a little more complicated with non-annual compounding periods.
3.5.1 Annual Percentage Rates (APR)
Banks and other credit providers disclose to consumers what is called an annual percentage rate (APR). The APR, otherwise known as the nominal rate, is the annualised interest rate using simple interest (thus without compounding!).
Let’s say you observe an interest rate of 10% on your bank's website for a credit card. This observed rate is what we call the quoted rate, or APR (it is required to be disclosed by law). Does this mean you pay 10% per year? Not necessarily. It depends on the compounding frequency. You find out that the interest rate is compounded monthly. This means you have actually only been provided with a monthly rate, which you have to calculate. How does that work??
VIDEO: Interest rates (YouTube, 2m20s)
To convert the APR into the variables for time value formulas, APR is divided by the number of compounding periods per year to get the “periodic” interest rate, or the interest rate per compounding period to get r for the PV or FV formula. And the number of years is multiplied by the number of compounding periods per year to get the n for the time value formulas.
Let’s consider quarters as an example:
Suppose we have a time value problem that runs for five years and has an APR of 12%, compounded quarterly. If we have quarterly cash flows that run for 5 years, what is our r and n?
The r rate for that period is 12%/4=3%. The time dimension (=n) of the problem is 20 quarters rather than five years (5 years x 4 quarters/year = 20 quarters). Hence r and n for the problem should be 0.03 and 20, respectively.
Exercise
Match the APR and compounding frequency to r and n :
Example
Your bank offers you a "special" student loan to buy your new $1400 laptop for your studies. The interest rate is 8% p.a. compounded weekly. You plan to pay back the loan in full, in one payment, in 5 years time. How much do you owe the bank then?
This question is asking about the future value of your loan. The present value is $1400, your interest rate per period (weeks)r is 0.08/52, and your total number of periods (weeks)n is 5*52.
[latex]FV^{5\ast52}=$1400\times\left(1+\left(\frac{0.08}{52}\right)\right)^{5\ast52}[/latex]
[latex]FV^{260}=$2,087.91[/latex]
Thus, you owe the bank $2087.91 in 5 years time.
3.5.1.1 More examples of compounding periods and interest rates
VIDEO: Compounding frequencies (YouTube, 2m20s)
3.6 Equivalent Interest Rates
3.6.1 Working with Different Compounding Frequencies
Often we need to compare different investments, and as we’ve seen, not all interest rates are quoted the same way. Compounding frequency matters. For a 12% APR, would you rather borrow with quarterly compounding or fortnightly compounding? How would you compare?
Let’s consider the credit card from the last section. Remember that the APR is 12% and compounding is monthly. You charge $100 on the card at the beginning of the year. At the end of the year, you go to pay off the credit card balance as planned. It seems reasonable to assume that with an APR of 12%, your credit card balance at the end of one year would be $112 (1.12 × $100 = $112). Is that right? Wrong! The bank is actually charging you 1% per month, meaning that the bank will compound your credit card balance monthly, 12 times over the year. The bank’s calculation for the balance due is $112.68 ($100 × 1.0112 = $112.68). The bank is actually charging you 12.68% per year, and the total interest paid for the 1-year loan is $12.68 rather than $12. This simple example raises a question: What is the correct way to annualise an interest rate?
VIDEO: Introduction to EAR (YouTube, 3m3s)
3.6.2 Computing the Effective Annual Interest Rate
Given the credit card example above, we can conclude that when interest on your investment or loan is paid more frequently than once a year, you may in fact be earning (or paying) a higher rate of interest on your savings than the quoted rate given to you by your financial institution. Every interest rate quoted has a compounding frequency associated with it. If this is not stated explicitly confusion can (and often does) arise about exactly what that interest rate means.
VIDEO: Calculating the EAR (YouTube, 2m40s)
The Effective Annual Interest Rate (EAR) is an important tool that allows the evaluation of the true return on an investment or true interest rate on a loan. More specifically, EAR is defined as the annual growth rate that takes compounding into account. Mathematically, the EAR can be stated as follows:
where
m = the number of compounding periods during a year
APR = quoted or nominal interest rate
The EAR conversion formula accounts for the number of compounding periods, and thus effectively adjusts the annualised quoted interest rate for the time value of money. In the case of compounding more frequently than once per year, the EAR is always higher than the stated annual interest rate. Because EAR is the true cost of borrowing and lending, it is the rate that should be used for comparing different investment options. Note however that simply converting the APR to the EAR does not take fees into account which should be considered when deciding between investment options (more on this in Chapter 4!).
We will use our earlier bank credit card example to illustrate the EAR equation. Recall that the credit card has an APR of 12% (1% per month). The APR is the quoted interest rate, and the number of compounding periods per year (m) is 12. Applying the EAR equation, we find that the effective annual interest rate is:
[latex]=\left(1+\frac{0.12}{12}\right)^{12}-1[/latex]
[latex]=\left(1.01\right)^{12}-1[/latex]
[latex]=1.1268-1= 0.1268\:or\:12.68\%[/latex]
The EAR of 12.68% is the true cost of borrowing the $100 on the bank credit card for one year. The calculation adjusts for the effects of compounding and, hence, the time value of money.
Finally, notice that interest rates are quoted in the marketplace in three ways:
- The quoted interest rate (APR). This is an interest rate that has been annualised by multiplying the rate per period by the number of compounding periods per year.
- The interest rate per period (periodic interest rate). The bank credit card rate of 1% per month is an example of this kind of rate. You can find the interest rate per period by dividing the quoted interest rate by the number of compounding periods per year.
- The effective annual interest rate (EAR). This is the interest rate actually paid (or earned) over a year, which takes compounding into account. Sometimes, it is difficult to differentiate a quoted interest rate from an EAR. Generally, however, an annualised consumer rate is an APR rather than an EAR.
Example
Suppose you are the Chief Financial Officer (CFO) of Infigen Energy. Your firm is planning a $1 billion solar farm expansion and will finance it by borrowing money for 5 years. Three banks have submitted interest rate quotes, all are APRs:
- Westpac: 10.40% compounded monthly
- Commonwealth Bank: 10.90% compounded annually
- ANZ: 10.50% compounded quarterly
Although all the loans have the same maturity, the loans are not comparable because the APRs have different compounding periods. To make adjustments for the different time periods, we apply the EAR equation to convert each of the APR quotes into an EAR:
Westpac:
[latex]EAR=\left(1+\frac{0.1140}{12}\right)^{12}-1[/latex]
[latex]=\left(1.0087\right)^{12}-1[/latex]
[latex]=\left(1.1091\right)-1[/latex]
[latex]=0.1091,\:or\: 10.91\%[/latex]
Commonwealth:
[latex]EAR=\left(1+\frac{0.1090}{1}\right)^1-1[/latex]
[latex]=\left(1.1090\right)-1[/latex]
[latex]=0.1090,\:or\: 10.90\%[/latex]
ANZ:
[latex]EAR=\left(1+\frac{0.1050}{4}\right)^4-1[/latex]
[latex]=\left(1.0263\right)^4-1[/latex]
[latex]=\left(1.1092\right)-1[/latex]
[latex]=0.1092,\:or\: 10.92\%[/latex]
As shown, Commonwealth Bank offers the lowest interest cost at 10.90%.
Notice the shift in rankings that takes place as a result of the EAR calculations. When we initially looked at the APR quotes, it appeared that Westpac offered the lowest rate and Commonwealth had the highest. After calculating the EAR, we find that when we account for the effect of compounding, Commonwealth actually offers the lowest effective interest rate.
Another important point is that if all the interest rates are quoted as APRs with the same compounding frequency, such as monthly, the interest rates are comparable, and you can select the correct rate by simply comparing the APRs. That is, the lowest APR corresponds with the lowest cost of funds. Thus, it is correct for borrowers or lenders to make economic decisions with APR data as long as interest rates have the same maturity and the same compounding period. To find the true cost of the loan, however, it is still necessary to calculate the EAR.
Exercise
Test your knowledge: Rank the best interest rate
You have $5,000 to invest for five years. You have the following alternatives (all are for a 5 year period and have the same level of risk). Rank the investment based on return.
3.7 Summary
This chapter has introduced the basic principles of a very important concept in finance: the time value of money. The basic equations for present value and future value equations are two of the most fundamental relationships in finance and will be applied throughout the remainder of this course.
- Timelines are a critical first step in organizing cash flows in a financial problem.
- There are three rules of time travel:
- Only cash flows that occur at the same point in time can be compared or combined.
- To move a cash flow forward in time, you must compound it.
- To move a cash flow backward in time, you must discount it.
We also learnt that the concept of compounding does not only occur in financial settings. A variable growing at a constant rate (=compounding) occurs in many different settings, and thus we can use the same formula to find out, for example, at what rate a population has been growing. It was shown how our socio-economic systems have been growing exponentially over the past 50 years has caused rapid changes in our natural environment.
Finally, we discussed the importance of interpreting interest rates appropriately. Interest rates are often quoted as Annual Percentage Rates (APRs), compounded at a certain frequency. From this information we can find: 1) r and n for our time value of money calculations and 2) the EAR for comparing different interest rates with different compounding frequencies.
In this chapter we applied the time value of money concept to a single cash flow, next chapter we will apply the concept to multiple cash flows.
Note that the “discount rate” can also be used to compound.
3.7.1 Key Formulas
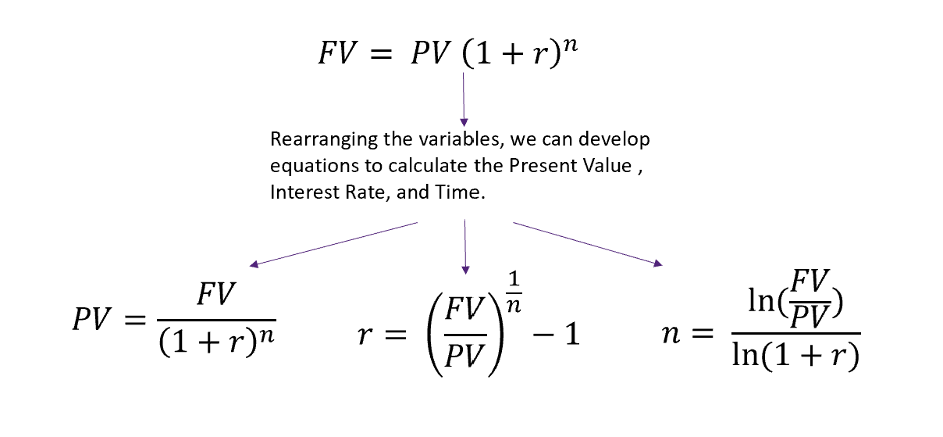
where:
- Future Value (FV): the value at the end of a specific period
- Present Value (PV): the value of the beginning of a specific period
- Number of periods (n): the number of periods.
- Interest rate (r): the interest/growth rate per period.
NOTE: In each time value of money problem, it is important to first draw a timeline. This will help you to identify which variable you are trying to solve for and what the values are for each of the other variables. Both the Present Value and Future value are also a Cash Flow, where the present value is the Cash Flow at time 0 and the Future Value is the Cash Flow at time n.
Where:
m = the number of compounding periods during a year
APR = quoted or nominal interest