Introduction

A scale is an ordered collection of notes, uniformly ascending or descending.  Most scales separate their adjacent notes by either tones or semitones, and most scales replicate the pattern of tones and semitones in successive octaves.  The basic form of such scales resides within a single octave, with the starting note and ending note belonging to the same pitch class. E.g. C–D–E–F–G–A–B–C, or A–B–C–D–E–F–G–A.

In Western common-practice music, there are two main types of scale: the major scale and the minor scale.  These are both examples of diatonic scales.

A diatonic scale is one which uses seven notes before returning to the starting note an octave higher (or lower), and in which a note for each letter name (inflected or uninflected) is heard exactly once before the pattern resumes an octave higher or lower.

To start off, it is easiest to demonstrate this with the white key notes on the piano keyboard. Depending on the note on which we start our ordered series, the pattern of tones and semitones between adjacent notes will be different (see Example 1).

Example 1: Diatonic modes using white-key notes showing the different tone-semitone series for each mode.

In Example 1, the location of tones (shown in blue) and semitones (shown in red) does not change (semitones remain between E and F, B and C), but as we shift the point of reference, the order rotates.  Because there are seven white-key notes, there are seven different rotations of tones and semitones.

Modes

We call the different tone-semitone rotations shown in Example 1 modes. Each mode has a name that derives, originally, from Greek.  These are shown in Example 1 on the lower right area. Two of the modes, Ionian and Aeolian correspond to the common-practice major and (natural) minor scales.

Transposing modes

Any of these modes can be transposed—that is shifted to start on a different starting note.  To do so, we have to preserve the order of tones and semitones, and this means using the black-key notes as well as the white-key notes.  For example, if we wish to play or sing the Ionian mode starting on D, we will need to use F♯ and C♯ instead of F and C.  Likewise, should we wish, for example, to play or sing the Phrygian mode on G, we would need to use A♭ instead of A, B♭ instead of B and E♭ instead of E, in order to preserve the exact series of tones and semitones for the Phrygian mode.  These two examples are shown below (Example 2).  

Example 2: Two transpositions of modes showing how black-key notes are needed to preserve the specific tone-semitone series of the given mode.

We name modes by the starting note, followed by the name of the mode. E.g. “G Lydian,” or “A Mixolydian” When we talk about modes, the starting note is usually call the final.  Later, when we talk about major and minor scales, we will cal this starting note the tonic.

Major scales

The major scale corresponds to the Ionian mode. It can be played using the white-key notes exclusively by playing it starting on C.  In example 2, above, we have already seen how if we transpose the major scale to start on any note other than C, we have to start using black-key notes as well in order to preserve the tone and semitone rotation unique to the major scale.  The example below gives some examples of different transpositions of the major scale, using both the keyboard and staff notation (Example 3). As for the modes, we name the scale after its first note, or tonic.

Major scales over more than one octave

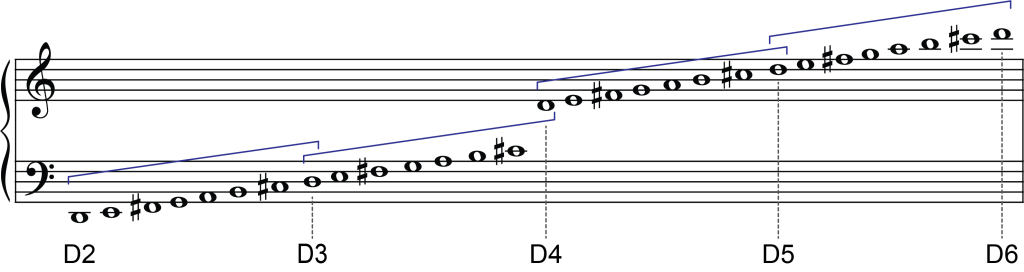
The examples of scales we have looked at have spanned only one octave.  Scales can extend over two or more octaves.  Essentially, when this happens we are simply overlapping scales starting on the same pitch class. The example below shows a D-major scale spanning four octaves, using the great staff.

Example 5: D-major scale over four octaves from D2 to D6 using the great staff.  Each overlapping octave is bracketed.

Scale degrees

Each note of a major scale is known as a degree.  We can refer to these degrees in several ways:

• Scale-degree numbers, written as Arabic numerals with a caret (^)
• Scale-degree names (we already know that the first degree of the major scale is called the tonic)
• Tonic sol-fa syllables, used for singing using a moveable “do” system

These are all listed below in ascending order.  The tonic is listed twice, as it is the first degree of the scale, and therefor forms the bounding octave.  We might refer to as a “lower” tonic and and as and upper tonic.  As far as pitch class is concerned, in any given scale, and are equivalent.

Scale degree number	Scale degree name	Tonic sol-fa syllable
	tonic	do
	leading note	ti
	submediant	la
	dominant	so
	subdominant	fa
	mediant	mi
	supertonic	re
	tonic	do

Importantly, all the above move in relation to the starting pitch of the scale. They are not attached to any specific pitch outside of the limits of the scale. Below are three different major scales—C major, B♭ major, and E major. You will see how, despite the pitch changing for each scale, the scale-degree number, name and sol-fa syllable keep the same relative positions.

Tetrachords

A tetrachord is a four-note contiguous set of notes from a scale.  When we divide a scale by tetrachords we refer to the lower and upper tetrachord.

• Lower tetrachord includes the tonic (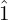), supertonic (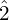), mediant (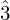) and subdominant ()
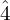• Upper tetrachord includes the dominant (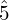), submediant (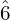), leading note^[1] (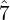) and (upper) tonic ().

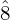Scales and keys

In Western common-practice music, key is a fundamental concept which relates to the system of tonality.  Key refers to the way in which a hierarchy of structural importance and relative stability is conferred on certain notes of a scale. Primarily, in tonal music, the tonic of a scale tends to be experienced as the location of highest stability, as a place where music can come to rest without an innate feeling in the listener that it should or must continue.  Consider Example 8, below.

In the score for this example, the left-hand (lower staff) part of the piano is made smaller so that we can focus on the melody (upper staff) where we have added both sol-fa syllables (below) and scale-degree numbers (above).  With one minor exception, all the pitch-content in these bars of music belongs to the scale of B♭ major.  This is clarified by the scale provided for reference below the score.  

You might notice that the bars 1–2 and 5–6 are very similar, but that bars 3–4 and 7–8 follow different paths.  In bars 1–4, despite some ups and downs, the overall contour of the melody is an overall descent from the dominant ( or so) to the supertonic ( or re).  In bars 5–8, which start out the same way, the contour of the melody takes up from the dominant to the tonic ( or do).

If you listen to or play just the melody of these two phrases separately, you will probably notice that the second phrase sounds more “finished” than the first.  Try it using a piano, or the players below.

Somehow, the first phrase’s ending is not quite as satisfying as the second, it has an implication that the music should continue (even if it doesn’t). By contrast, the second phrase sounds like the music can stop with out further need to go on (even if it does).

The second phrase’s ending on the tonic degree ( or do) is one of the factors that confers its greater sense of conclusiveness and stability.  This sense of stability on the tonic degree gives it a fundamental position in the hierarchy of scale degrees and determines what we call the key.  In the case of Example 8, we can say that the key of the music is B♭ major, or that the music is in the key of B-flat major.  Another way of putting this is that the tonic of the music is B♭, or the piece is “in” B-flat major. 

Another feature worth noting is shown by the progression from the leading note ($\hat{7} or ti) to the tonic at the end of phrase 2, shown in the red enclosure marked (b).  In comparison to the tonic, the leading note is extremely unstable, and has a strong tendency to move toward the tonic, almost like a gravitational tug.  For this reason, we often think of the leading note as a “tendency note.”

Key signatures

Example 9 (below) shows the music of Example 8 in the way that Mozart originally wrote it.

The most obvious  difference between the notation of this music from Example 9 to Example 9 is that in Example 9, there are much fewer accidentals and that each staff has two flat signs immediately after the clef—one on the line for B♭ and the other in the space for E♭. This is call a key signature, and it indicates that all the notes on the staff that would otherwise be played as B and E, must now be played as B♭ and E♭, unless otherwise indicated. We call this particularly key signature the “key signature of B♭ major.”

Some important things to note about key signatures are:

• There is a specific order to the placement of accidentals in the key signature
• The key signature is repeated at the start (immediately after the clef) of every staff or system of staves (unlike time signatures)
• The accidentals in the key signature affect all notes of that pitch class.  E.g. a sharp sign (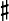♯) on the F line in the key signatures means than any note F is sharpened (unless otherwise indicated).

If a note that is included in the key signature needs to be altered, then an accidental is used and applies to that note and any other of the same note for the rest of the bar.  See the E natural (E♮) circled in red and marked (a) in Example 9.  (Note that the flat sign in the next bar in front of the E, marked (b), is not strictly needed, but is given as a courtesy to ensure clarity.)  

Here is another example, showing what the composer wrote and then a version without key signature, using all accidentals. The key of this music is B major, and this requires five notes (C, D, F, G and A) to be sharpened—as shown at the bottom of the example.

It should be clear from this that the use of the key signature, once you get accustomed to it, is much more convenient and efficient.

Circle of fifths

Given that we have seven white-key pitch classes and five black-key ones, we have twelve different major scales, each with a unique key signature. Getting to know all the key signatures can seem like a chore, but the concept of tonality and key, and therefore the use of key signatures, is deeply embedded in Western common-practice and this knowledge is central to musicianship.

Thankfully, there is a certain logic to the way key signatures work, and this involves an important theoretical construct known as the circle of fifths.  To create the circle of fifths, we start at C and move both up and down in perfect fifths (that is seven semitones).  If we do this in a line, it looks like this:

G♭ – D♭ – A♭ – E♭ – B♭ – F – C – G – D – A – E – B – F♯

You will notice that at either end of this line we have notes that are enharmonically equivalent—G♭ and F♯. That is, they both stand for the same pitch class.  The circle of fifths takes this line and wraps it around a circle so that these equivalent versions of the same pitch class meet and overlap.  It produces a clock face, in which each of the twelve different pitch classes is represented once. If we travel clockwise around the circle, then we move up by perfect fifths (↑P5), and if we move anti-clockwise, we move down by perfect fifths (↓P5).  

If we take these pitch classes around the circle as the tonic scale degrees of keys, then we will notice a pattern in the key signatures:

• Starting at C major, as we go around the circle in a clockwise direction we progressively add sharps to the key signatures.
• Starting at C major, as we go around the circle in an anti-clockwise direction we progressively add flats to the key signatures.

Also, by the same token, if we start at the opposite pole, G♭/F♯ major:

• As we go clockwise we progressively take flats away
• As we go anti-clockwise we progressively take sharps away

The circle of fifths also provides information on what sharps and flats are added.  The shaded arc in Example 10 encloses the seven uninflected or white-key note names.  We find that these same letter names reading clockwise through this arc (F–C–G–D–A–E–B) indicate the order we add sharps—G major has F♯, D major has F♯ and C♯, and so on.  Similarly, if we read it anti-clockwise (B–E–A–D–G–C–F), the letter names indicate which flats we add—F major has B♭, B-flat major has B♭ and E♭, and so on.