11 Organising Pitch: Triads
Introduction
A triad is a specific type of three-note chord. In its simplest form it comprises three notes stacked one above the other such that we have two thirds between each successive note and a fifth between the outer notes. Triads are one of the main building blocks of Western common-practice harmony.
The most basic form of the triad is shown in Example 00, below. Each note of a triad has a specific name. The lowest note is called the root, the note in the middle is called the third (because it is a third higher than the root), and the note at the top is called the fifth (because it is a fifth higher than the root).
Triads can appear, as above, in harmonic form, where all notes are given simultaneously. They can also be arranged melodically, with the notes presented in succession. This is called arpeggiation (Example 00). There are a number of ways to arpeggiate a triad, the most obvious being from the bottom upwards (a), or from the top downwards (b). However, a number of permutations are possible because there are three notes to draw from (c) to (f).
It is important to note that, no matter what the order of the arpeggiation, the notes comprising the root, third and fifth, remain the same.
The arpeggiation of triads is a common feature of music. In classical music for keyboard, for example, one of the most (in)famous examples of arpeggiation is an idiomatic texture called the “Alberti bass”—named after the eighteenth-century composer Domenico Alberti (1710–1746), who used it quite extensively (although he did not, as is sometimes claimed, invent it). Basically, the Alberti bass is a device that enables continued sustaining of the notes of a triad that would otherwise die-away quite quickly after being struck as a single block chord. Usually, it appears in the left-hand part accompanying a melody in the right-hand part—see Example 00.
Example 00: Domenico Alberti, Sonata per cembalo in C major, op. 1, no. 3, first movement, bars 1–2.
Naming Triads and Triad Quality
Triads are identified by two elements:
- The triad’s root, expressed as a pitch-class.
- The triad’s quality, which can be major, minor, diminished or augmented.
The quality of a triad is determined by the intervals between all three notes. There are three intervals in any triad (refer to Example 00):
- A lower third—formed between the root and the third
- An upper third—formed between the third and the fifth
- A fifth—formed between the root and the fifth
The lower and upper thirds can be major or minor and the fifth can be perfect, diminished or augmented. However, these can only occur in certain combinations, as shown below.
Example 00: Configuration of intervals in different triad qualities.
Following this, an “A major triad,” for example, would have the note A as its root, its third would be C![]() (a major third above A), and its fifth wo>uld be E (a minor third above C
(a major third above A), and its fifth wo>uld be E (a minor third above C![]() and a perfect fifth above A). Similarly, a “B minor triad” would have B as its root, its third would be D (a minor third above B), and its fifth would be F
and a perfect fifth above A). Similarly, a “B minor triad” would have B as its root, its third would be D (a minor third above B), and its fifth would be F![]() (a major third above D and a perfect fifth above B). Some examples are given below, using music notation.
(a major third above D and a perfect fifth above B). Some examples are given below, using music notation.
Chord symbols
In writing the names of triads, we can write them out in full (“D-flat major triad,” “F diminished triad,” “C minor triad,” and so on), or, often more frequently, we can use abbreviations, called chord symbols.
- A letter on its own indicates a major triad
- A letter followed by a lower case m indicates a minor triad
- A letter followed by a degree sign indicates a diminished triad
- A letter followed by a plus sign indicates an augmented triad
This is shown in the examples above.
Unfortunately, chord symbols are not necessarily standardised. The following table sets out the abbreviations used in this book (which are fairly common) and other alternatives which you might come across in other books or sites. We have used A as the root, but any letter or letter+accidental can be substituted.
| full name | chord symbols used here | other chord symbols |
| A major | A | [none] |
| A minor | Am | Amin | a | A- |
| A diminished | A° | Adim | Am♭5 | Am-5 |
| A augmented | A+ | Aaug | A♯5 |
Triad inversions—changing bass notes
Triads in their simplest form have the root at the lowest position. We call the note at the bottom of any chord (including triads) the bass note. However, it is possible to reorganise the order of notes so that either the third or the fifth may appear the bass note. These are called inversions. In a similar way to intervals, inversions involve one or more notes moving up or down an octave while others stay fixed. The nomenclature for these different arrangements is as follows:
- Root position—the root is the bass note
- First inversion—the third is the bass note
- Second inversion—the fifth is the bass note
In Example 00, below, the process of creating inversions in shown in two ways. In the upper line, se take the bass note and move it an octave higher each time, going from root position, to first inversion, to second inversion. In the lower line, we do the reverse.
Remember: When inverting a triad, we are not changing the pitch-class identified as the root, third or fifth. For instance, for an F major triad in first inversion, F is still the root, A is still the third, and C is still the fifth. However, A will be now be the bass note.
Labelling Inversions using chord symbols
There are two nomenclature systems for identifying inversions:
- Chord symbols using a slash and the name of the bass note.
- Figured bass
Figured bass is more common in classical music and is frequently used together with the Roman-numeral system of chord analysis which is introduced a little further down.
Chord symbols are more common in popular music and jazz. Because our focus in this book is on Western common-practice music, we will mainly used figured bass. However, getting to understand the method using chord symbols is important for being able to think in different styles and contexts. It is also an easier system to grasp. Below, are some examples of triad inversions using chord symbols.
Diatonic Triads
A diatonic triad is a triad comprising notes from the diatonic collection.
A triad can be constructed on any degree of a scale, using that degree as the root and then taking notes of the scale a third and fifth above that root to complete the triad.
For instance, in a major scale starting on the tonic (![]() , or do) we add the mediant (
, or do) we add the mediant (![]() , or mi) and the dominant (
, or mi) and the dominant (![]() , or so) to create a triad. Because the root of this triad is the tonic degree, it is called the tonic triad.
, or so) to create a triad. Because the root of this triad is the tonic degree, it is called the tonic triad.
We name diatonic triads after the name of the degree that is the root of the triad.
The next thing to note that is diatonic triads will have different qualities because of their position on the scale. For example, the tonic triad in a major key is a major triad, because do to mi is a major third and mi to so is a minor third (and do to so is a perfect fifth). However, the supertonic triad in a major key is a minor triad—re to fa is a minor third and fa to la is a major third (re to la is a perfect fifth).
In Example 00, below, we have set out the range of triad qualities for major and minor (natural and harmonic) scales using sol-fa syllables. This is done using five-note segments of the scale, working from the tonic upwards in each case, and showing the interval qualities of the thirds and fifths in each case. To help make it a little clearer, we have colour-coded the triad qualities—red for major, blue for minor, green for diminished and yellow for augmented (which only appears once, in the harmonic minor).
From the example above we can see that for the major and natural minor scales there are three major triads, three minor triads and one diminished triad. There is no augmented triad possible in the natural diatonic collection.
| major scale | natural minor | |
| triads (degrees as root) | triad quality | triad quality |
| leading note / subtonic | diminished | major |
| submediant | minor | major |
| dominant | major | minor |
| subdominant | major | minor |
| mediant | minor | major |
| supertonic | minor | diminished |
| tonic | major | minor |
In introducing the leading note as part of the harmonic minor, we introduce a second diminished triad, as well as an augmented triad, these replace the major triads in the natural minor scale that are rooted on the mediant and subtonic, respectively. The minor dominant triad is now major.
| harmonic minor | |
| triads (degrees as root) | triad quality |
| leading note | diminished |
| submediant | major |
| dominant | major |
| subdominant | minor |
| mediant | augmented |
| supertonic | diminished |
| tonic | minor |
As is explained in other parts of this book, there are a variety of rules and tendencies around which version of the minor scale to use for triads. In general you will find that in minor keys:
- The mediant triad is almost always constructed from the natural minor. Use of the augmented triad on the mediant is extremely rare in common practice.
- The dominant triad is mostly constructed from the harmonic minor and is therefore a major, not minor, triad in most cases. In a limited range of contexts, the minor version of the dominant can be used.
- The use of the leading note triad (from the harmonic minor), which is diminished, is quite common, as is the use of the subtonic triad (from the natural minor), which is major, but the contexts in which they are used are entirely different and they are not interchangeable.
Roman numerals
Elsewhere we explain how degrees of the scale can be referred to by numbers, using an Arabic number with a caret (![]() ,
, ![]() ,
, ![]() , etc.).
, etc.).
When it comes to triads, we can also number them, but now we use Roman Numerals, as in I, II, III etc.
A Roman numeral locates the root of a diatonic triad according to the scale degree. So, for instance, the Roman numeral I indicates the tonic triad—i.e. the diatonic triad whose root is ![]() .
.
A chord symbol locates the root of a triad to a specific pitch class, independent of any scale or key.
For example, A–C♯–E is always given by the chord symbol A, but its Roman numeral will vary depending on the key that it is found it. So, in the key of A major, it will be I, but in E major, it will be IV.
Both systems have advantages and disadvantages. However, in tonal music the Roman numeral system is useful in being key independent (like scale degree numbers and sol-fa syllables) meaning the same chord progression in different keys will be represented the same way in Roman numerals and we can more easily understand the relationship between chords.
It has become standard practice to alter the case of Roman numerals to reflect the quality of the diatonic triads they stand for.[1]
- Major triads are given in upper-case Roman numerals—e.g., I, III, V, etc.
- Minor triads are given in lower-case Roman numerals—e.g. i, iv, vi, etc.
- Diminished triads are given in lower-case Roman numerals with a degree sign—e.g. ii°, vii° etc.
- Augmented triads are given in upper-case Roman numerals with a plus sign—e.g. III+, V+, etc.
In Example 00, below, we give all diatonic triads for major and natural and harmonic minor, using D as tonic.
Example 00: Roman numerals for diatonic triads on all degrees of the scale, for major, natural minor and harmonic minor scales (using D as tonic)
Inversions and Figures
In Western common-practice music, triad inversions (and inversions of other chords) are indicated using figures. Figures are Arabic numerals which provide a short hand for the intervals formed above the bass note of the triad.
- Root-position triads have notes a third and a fifth above the bass note.
- First-inversion triads have notes a third and a sixth above the bass note.
- Second-inversion triads have have notes a fourth and a sixth above the bass note.
Hence:
- Figuring for root position is:
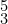
- Figuring for first inversion is:
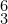
- Figuring for second inversion is:
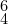
These figures are placed directly beneath the triad in question, as shown in the example below. The figures are always stacked vertically and the higher number is always at the top.
Example 00: Figuring for triads in root position, first inversion and second inversion (bass notes shown in red).
Abbreviated figures
The figuring shown in Example 00, above, is “full figuring” in that both intervals above the bass note are included. In common practice, it is standard to use abbreviated figuring. For triads, this is as follows:
- Root position—no figuring is shown,
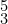 is assumed
is assumed - First inversion—only
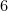 is shown,
is shown, 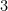 is assumed.
is assumed. - Second inversion—full figuring is shown (
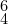 )
)
Example 00: Abbreviated and full figuring for triads in root position, first inversion and second inversion (bass notes shown in red).
Realising figures
Figures not only describe inversions of triads and other chords, they can be used to produce them. A single note with figures can be realised by adding the notes implied by the figures. Remember, figures tell us about intervals above the bass note. In the example below, we have relised figuring for the bass notes E—Example 00 (a) to (c)—and D—Example 00 (d) to (f).
You might note, also, that in Example 00 (f), accidentals can be prefixed to figures, telling you to alter the note(s) determined by the relevant figures in the same way. In Example 00 (f), the ![]() before the figure 4 tells us to write a G
before the figure 4 tells us to write a G![]() . G is a fourth above D, and the
. G is a fourth above D, and the ![]() tells us, therefore, to add a sharp sign to this G.
tells us, therefore, to add a sharp sign to this G.
How figured bass notes can be realised.
In Example 00, above, we have just shown the minimal realisation for figures. Figures, however, do not tell you exactly what pitches to realise above a bass note, they only tell you the pitch classes resulting from the intervals indicated. In the example below, all the chords on the outside are accurate realisations, in different contexts, of the figured bass note in the centre.
What we can see from the example above is that all the realisations on the outside:
- the bass note (that is, the lowest note) is always C
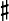 , that is, the note given in the figured bass.
, that is, the note given in the figured bass. - the notes above the C
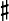 are always E (a third above C
are always E (a third above C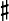 ) and A (a sixth above C
) and A (a sixth above C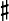 ), but they are not limited to the E and A immediately above the C
), but they are not limited to the E and A immediately above the C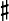 , nor must A always be above E, and in some cases, one of them is doubled—represented twice.
, nor must A always be above E, and in some cases, one of them is doubled—represented twice.
The figured bass is just a basic prescription, showing the pitch-class content that must appear above the bass note, but its actually realisation is context dependent.
Figured bass—A Historical note
During the Baroque period of Western music history, which is usually understood to comprise the seventh century and the first half of the eighteenth, the use of figures was almost ubiquitous in all music.
It was standard practice for most music to have an underlying part designated basso continuo (literally, “continuous bass”), often abbreviated continuo. This was always the lowest sounding part, and in notation was typically the lowest staff in a score. Its instrumentation was non-specific, but customarily more than one instrument played this part. This might include a low string instrument—such as cello, viola da gamba, or violone—and an instrument capable of playing chords—such as harpsichord, organ, or theorbo. It often have a whole group of instruments.
This basso continuo part was always given as a figured bass. That is, a single staff, usually with bass clef, with notes also supplied with figures. It was the job of the harpsichordist (or organist, or theorbist, etc.) to realise chords above the bass line relying on the figures.
In other words, the figures did not tell the play exactly which notes to play, but rather to play notes placed as they deemed appropriate in accordance with the intervals indicated. For example, a bass note F![]() with the figure
with the figure ![]() would demand A and D, but exactly which A and which D, and whether they chose to double either one of them, was up to the player—so long as they were above the bass note.
would demand A and D, but exactly which A and which D, and whether they chose to double either one of them, was up to the player—so long as they were above the bass note.
The example below shows a few bars from an air (song) by the mid eighteenth-century composer Elisabetta de Gambarini. Two versions are shown. At the top is the original publication from c. 1748. This included two staves, the upper one for the singer and the lower one for the continuo accompaniment, including the bass line (that is, the melody in the bass) and figuring below the bass notes—this is the figured bass. At the bottom, a realisation is given in which the figured bass line has been “expanded” by showing the possible realisation of the chords implied in the figuring. This is not the only way to realise these figures, but it is conceivably what a harpsichordist might well have played reading from the figured bass.
Example 00: Elisabetta de Gambarini, “Behold, Behold and Listen,” from Lessons and Songs, op. 2, bars 45–50 (original publication, c. 1748, and transcription)

Figures and Roman numerals
Figures and Roman numerals can be used in conjunction with each other in the naming and analysis of triads in common-practice music. To indicate an inversion, the figure follows the Roman numeral as a suffix, and it is assumed that the abbreviated figures are being used.
For instance, if we are in the key of C minor, V would indicate the dominant triad in root position (G, B![]() , D), whereas V
, D), whereas V![]() indicates the dominant triad in first inversion (B
indicates the dominant triad in first inversion (B![]() , D, G) and V
, D, G) and V![]() indicates the dominant triad in second inversion (D, G, B
indicates the dominant triad in second inversion (D, G, B![]() ).
).
Some examples are show below in various keys.
Example 00: Diatonic triads in various keys and inversions with Roman numerals and figures.
- C major: subdominant triad in root position
- G minor: tonic triad in first inversion
- E minor: dominant triad in root position
- E major: supertonic triad in second inversion
- D minor: submediant triad in root position
- D major: dominant triad in first inversion
- F-sharp major: dominant triad in second inversion
- E-flat major: tonic triad in first inversion
- A minor: leading-note triad in first inversion
- B major: submediant triad in second inversion
In the example above, note the practice of identifying the key at the left followed by a colon. Upper case letters represent major keys (as in A: for “A major”) and lower case letters represent minor keys (as in g: for “G minor”). The Roman numerals are always placed below the staff, never above.
The process of using Roman numerals to identify triads in this way is often called “Roman-numeral analysis.”
Doing Roman numeral analysis—identifying triads in a simple musical texture.
Roman numeral analysis can be a powerful tool for summarising pitch content in music and understanding relationships between triads (and other chords). The first part of doing a Roman numeral analysis is simply to identify and annotate the score. In the video below, we go through this process using the music from Example 00, above.
⚠️Short video showing Roman numeral analysis.
In using Roman numerals together with figures, it is important to keep the following in mind:
- Unlike figured bass, which just uses figures alone, we do not find accidentals prefixed to the figures associated with Roman numerals, because the Roman numeral tells us the triad quality and thus the pitch content exactly. For example, in G minor, vii°6 includes A, C and F
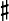 ; while the figuring alone above a bass note A would require the figure
; while the figuring alone above a bass note A would require the figure 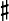 6, the
6, the 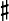 is not required before the 6 in vii°6 because from the Roman numeral vii° we know that the leading-note triad (in G minor: F
is not required before the 6 in vii°6 because from the Roman numeral vii° we know that the leading-note triad (in G minor: F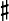 , A and C) is indicated, so in first inversion of this triad, F
, A and C) is indicated, so in first inversion of this triad, F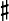 is understood.
is understood.
- The two elements, Roman numerals and figures, must still be understood to be conceptually distinct. The Roman numeral tells us about the root of the triad and its pitch content; the figures tell indirectly about the inversion and, thus, the bass note.
- This is often not the case in older texts, where Roman numerals are given exclusively in upper case irrespective of triad quality. ↵
A chord is any simultaneous combination of musical notes. Within chords as a class, there are also more specific kinds of chords with specific names, such as "dyad" (any two-note chord), "triad" (a three-note chord with notes related by the interval of a third), and so on.
An arpeggio is a chord presented with each of its notes in succession rather than simultaneously (block chord). Typically, this involves moving from the lowest note of the chord, successively upwards to the top note, or vice-versa. However, any succession of the chord notes could be considered an arpeggio. Sometimes the term "broken chord" is used to mean the same thing. Turning a block chord into an arpeggio is to "arpeggiate" it, in a process knowns as "arpeggiation."
A block chord is any chord in which all notes of the chord are played simultaneously.
A chord symbol is a form of notation that describes a triad, seventh chord, or other tertian harmony. It identifies the chord by naming the root, and supplying information about quality and inversion in abbreviated form. For example, "G" would indicate a G major triad, "B♭7" would indicate a dominant ("major-minor") seventh chord on B♭. "F♯ø7/C" would indicate an F-sharp half-diminished seventh in second inversion. There is some variability between different conventions in chord symbols. They should note be confused with Roman numerals.
A bass note is the lowest sounding note of a chord, in any texture. It typically determines what inversion a triad, seventh chord, or other tertian harmony is in.
