4 Time Value of Money (Part 2)
4.1 Introduction
At the end of this chapter, you will be able to:
- explain why cash flows occurring at different times must be adjusted to reflect their value as of a common date before they can be compared
- calculate the present value and future value for multiple cash flows
- identify an annuity, calculate the present value and future value of an ordinary annuity
- identify a perpetuity and calculate the present value of an ordinary perpetuity
- apply time value of money concepts to common financial decisions.
Have you ever thought about taking out a mortgage in a few years? Or maybe heard your parents talk about their retirement goal? For retirement, as people are living longer, we need to save more to fund those extra years in retirement. While we can estimate what retirees of today need in superannuation, it is difficult to project the amount needed for those retiring in 10, 15 or even more years, as there are too many variables relating to how the economy and investment world is likely to perform.
The value of a retiree’s superannuation fund largely depends on its earnings over a long holding period and how much is invested on an ongoing basis. It is important for individuals to adequately plan for retirement by keeping an eye on the value of their superannuation and making adjustments if it appears to be inadequate to meet their future needs.
This topic discusses the discounting and compounding of multiple cash flows and provides the tools that should help you to make informed financial decisions that involve multiple cash flows such as your retirement.
4.2 Comparing Multiple Cash Flows – Theory
4.2.1 Time Value of Multiple Cash Flows
The concepts we covered last week are summarised in the following video.
VIDEO: Time Value of Money Explained (YouTube, 2m48s)
In this chapter, we consider the value of multiple cash flows. Most business or even personal decisions involve a series of cash flows over time.
Imagine you own a pizza shop in Indooroopilly Shopping Centre. You are considering adding a production line and your accountant told you that the decision will require an analysis of the project’s expected cash flows over a number of periods. Initially, there will be large cash outlays to build and get the new line operational. Thereafter, the project should produce cash inflows for many years. Because the cash flows occur over time, the analysis must consider the time value of money, discounting each of the cash flows by using the present value formula we discussed in the previous topic. We also learnt that to compare cash flows, we have to convert them to the same point in time.
We begin our discussion of the time value of multiple cash flows by calculating the future value and then the present value of multiple cash flows. These calculations are nothing more than applications of the techniques from the previous topic.
4.2.2 Future Value of Multiple Cash Flows
In the previous topic, we worked through some examples that involved the future value of a lump sum of money invested in a savings account that paid a certain interest per year. But suppose you are investing more than one lump sum?
Let’s say you put $1000 in a bank savings account today and another $1000 one year from now. If the bank pays 8% interest per year, how much money will you have at the end of 2 years? If you add another $1000 at the end of 3 years, how much will you have in three years?
To solve this, we can use the future value equation:
separately for each of the two $1000 deposits.
VIDEO: Future Value of Multiple Cash Flows (YouTube, 2m39s)
First, let’s look at a timeline so that we can see the magnitude and timing of the cash flows.
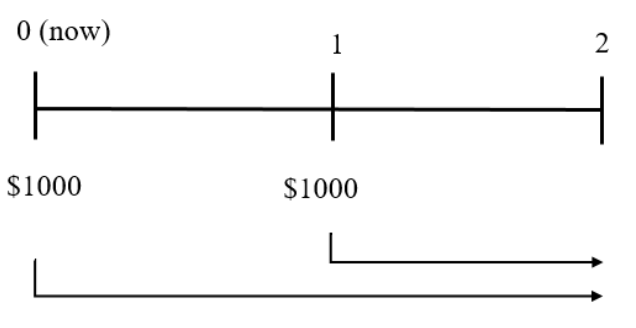
There are two cash flows into the savings plan. The first cash flow is invested for 2 years and compounds to a value that is calculated as follows:
[latex]FV_2=PV\times\left(1+r\right)^2[/latex]
[latex]=$1000\times\left(1+0.08\right)^2[/latex]
[latex]=$1000\times1.1664[/latex]
[latex]=$1166.40[/latex]
The second cash flow earns simple interest for a single period only and grows to:
[latex]FV_2=PV_1\times\left(1+r\right)[/latex]
[latex]=1000\times\left(1+0.08\right)[/latex]
[latex]=$1000\times1.08[/latex]
[latex]=$1080[/latex]
Therefore, the total amount of money in the savings account after 2 years is the sum of these two amounts, which is:
[latex]$2246.40\ \times($1166.40\ +\ $1080)[/latex]
Now suppose that you expand your investment horizon to 3 years by investing $1000 today, $1000 a year from now, and another $1000 at the end of 2 years. How much do you have at the end of 3 years?
Let’s draw a timeline to correctly identify the time period of each cash flow.
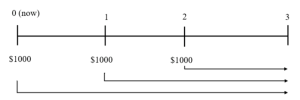
Now, we can calculate the future values of each of the individual cash flows.
[latex]FV_3=PV_2\times\left(1+r\right)=$1000\times\left(1+0.08\right)=$1000\times1.08=$1080[/latex]
[latex]FV_3=PV_1\times\left(1+r\right)^2=$1000\times\left(1+0.08\right)^2=$1000\times1.1664=$1166.40[/latex]
[latex]FV_3=PV0\times\left(1+r\right)^3=$1000\times\left(1+0.08\right)^2=$1000\times1.2597=$1259.71[/latex]
Adding up the future values, the total is $3506.11.
Our example suggests that instead of earning 8% simple interest on each $1000 investment, you are also earning interest on interest for the first and second interest received. To summarise, solving future value problems with multiple cash flows involves a simple process:
- Draw a timeline to ensure each cash flow for its time period are correctly identified.
- Calculate the future value of each cash flow for its time period.
- Add up the future values.
Let’s use this process to solve a practical problem. Suppose you have an investment that will pay you the following cash flows over the next five years: $4947, $5157, $6131, $4024, and $9549. If you invest these cash flows at an expected rate of 8.25% annually over the five years, what is the future value of your investment’s cash flows at the end of 5 years?
Step (1) Draw a timeline
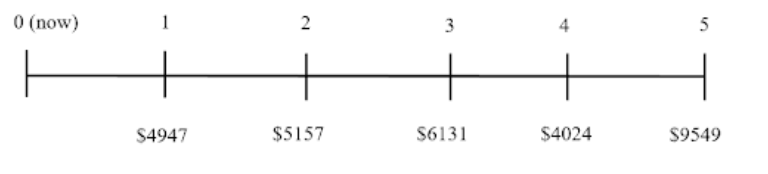
Step (2) Calculate the future values of each cash flow
[latex]FV5=4947\left(1.0825\right)^4+5157\left(1.0825\right)^3+6131\left(1.0825\right)^2+4024\left(1.0825\right)^1+9549[/latex]
Step (3) Add up all the future values
[latex]FV5=4947\left(1.0825\right)^4+5157\left(1.0825\right)^3+6131\left(1.0825\right)^2+40244\left(1.0825\right)^1+9549=6792.87+6541.55+7184.34+4355.98+9549[/latex]
[latex]=$34,423.74[/latex]
At the end of the fifth year, you will have $34,423.74.
Exercise
4.2.3 Present Value of Multiple Cash Flows
In many situations, we need to calculate the present value of a series of future cash flows. We do this, for example, to determine what we have to save every year to be able to withdraw at certain amount at a future date. This can be used to find the market price of a bond (Chapter 5), to decide whether to purchase a new machine or to determine the value of a business.
Solving present value problems involving multiple cash flows is similar to solving future value problems involving multiple cash flows:
First, we prepare a timeline to identify the magnitude and timing of the cash flows.
Second, we calculate the present value of each individual cash flow using
Finally, we add up the present values. The sum of the present values of a stream of future cash flows is their current market price, or value. There is nothing new here!
Let’s work through some examples to see how we can use present value equation to find the present value of multiple cash flows.
VIDEO: Present Value of Multiple Cash Flows (YouTube, 3m5s)
Now, let’s consider another example:
Suppose you have an opportunity to buy a small business while you are at university. The business involves selling sandwiches, home-made kombucha and snack foods to students from a truck that you drive around campus. The annual cash flows from the business have been predictable. You believe you can expand the business, and you estimate that cash flows will be as follows: $13,000 the first year, $11500 the second year, $12750 the third year, and $9635 the fourth year. You did some research at the university and found that an 8% discount rate would be appropriate.
How much should you pay for the business?
Step (1) Draw a timeline
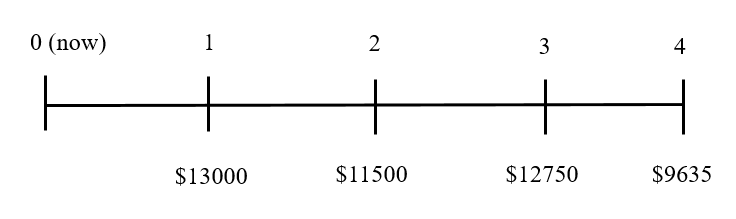
Step (2) Calculate the present values of each cash flow
[latex]P V_{0}=\frac{13000}{(1.08)}+\frac{11500}{(1.08)^{2}}+\frac{12750}{(1.08)^{3}}+\frac{9635}{(1.08)^{4}}[/latex]
Step (3) Add up all the present values
[latex]\begin{aligned} P V_{0} &=\frac{13000}{(1.08)}+\frac{11500}{(1.08)^{2}}+\frac{12750}{(1.08)^{3}}+\frac{9635}{(1.08)^{4}} \\ &=12037.04+9859.40+10121.36+7082.01 \\ &=\$ 39,099.81 \end{aligned}[/latex]
This calculation tells us that the value of the business is $39,099.81. If you pay $39,099.81 for the business, you will earn a return of exactly 8%. Of course, you should buy the business for the lowest price possible; however, you should not pay more than $39,099.81. If you do, you will be paying more for an investment than it is worth.
Let’s test your knowledge before you go on…..
Exercises
1. What is the key economic principle involved in calculating the present value and future value of multiple cash flows?
2. What are the steps involved in calculating the future value when you have multiple cash flows?
3. Explain why cash flows occurring at different times must be adjusted to reflect their value as of a common date before they can be compared, and calculate the present value and future value for multiple cash flows.
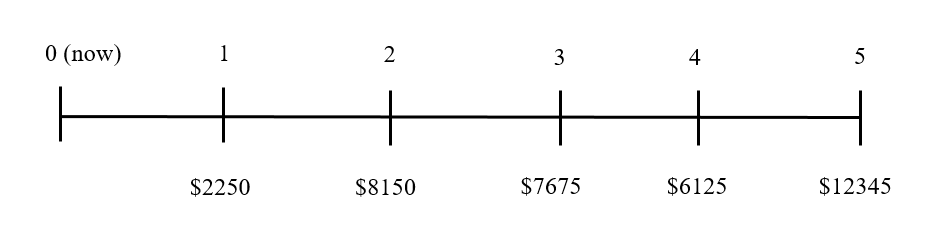
4. Your grandmother has agreed to deposit a certain amount of money each year into an account paying 7.25 per cent annually to help you go to university. Starting next year, and for the following 4 years, she plans to deposit $2250, $8150, $7675, $6125, and $12 345 into the account. How much will you have at the end of the 5 years?
The timeline for the cash flows and their future value is as follows:
4.3 Annuities – Present Value
4.3.1 Present Value of an Annuity
4.3.1.1 Motivation
We often encounter contracts that call for the payment of equal amounts of cash over several time periods. For example, most business loans and insurance policies require the holder to make a series of equal payments, usually monthly.
Similarly, nearly all consumer loans, such as car, personal, and home loans, call for equal monthly payments. Let's define some terms:
- Any financial contract that calls for equally spaced and level cash flows over a finite number of periods is called an annuity.
- If the cash flow payments continue forever, the contract is called a perpetuity.
- Most annuities are structured so that cash payments are received at the end of each period. Because this is the most common structure, these annuities are often called ordinary annuities.
We frequently need to find the present value of an annuity (PVA). Suppose, for example, that a financial contract pays $1000 at the end of each year for 3 years and the appropriate rate is 8%. The timeline for the contract is:

What is the most we should pay for this annuity? Using our usual present value equation of ...
[latex]PV_{0}=\frac{F V}{(1+r)^{n}}[/latex]
...all we need to do is calculate the present value of each individual cash flow ([latex]CF_n[/latex]) and add them up.
Simply do as follows,
[latex]\begin{aligned} P V_{0} &=\frac{F V} {(1+r)^{1}}+\frac{F V} {(1+r)^{2}}+\frac{F V} {(1+r)^{3}} \\ & =\ \frac{$ 1000} {(1+0.08)^{1}}+\ \frac{$ 1000}{(1+0.08)^{2}} +\ \frac{$ 1000}{(1+0.08)^{3}} \\ &=\$ 925.93+\$ 857.34+\$ 793.83 \\ &=\$ 2577.10 \end{aligned}[/latex]
This approach to calculating the present value of an annuity works as long as the number of cash flows is relatively small. In many situations that involve annuities, however, the number of cash flows is large, and doing the calculations by hand would be tedious. For example, a typical 20-year home loan has 240 monthly payments (12 months x 20 years = 240 months).
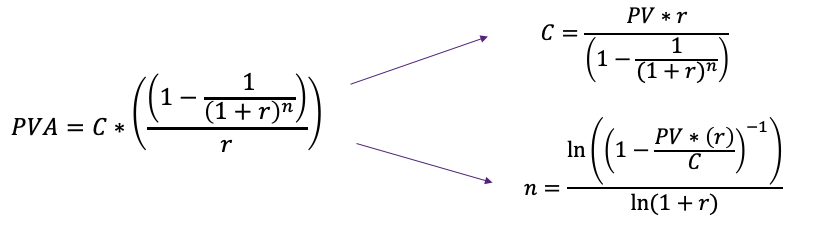
Fortunately, our problem can be simplified because the cash flows ([latex]𝐶𝐹_𝑛[/latex]) for an annuity are all the same. ([latex]𝐶𝐹_1=𝐶𝐹_2=𝐶𝐹3_=…=𝐶𝐹_𝑛=𝐶𝐹[/latex]). Thus, the present value of an annuity ([latex]PVA[/latex]) with n equal payments at interest rate r is the sum of the individual present value calculations:
[latex]PVn=CF\left(1+r\right)^1+CF\left(1+r\right)^2+\ldots\ldots\ldots+CF\left(1+r\right)^n[/latex]
Note that each [latex]CF[/latex] is essentially a future value that is being discounted to its present value.
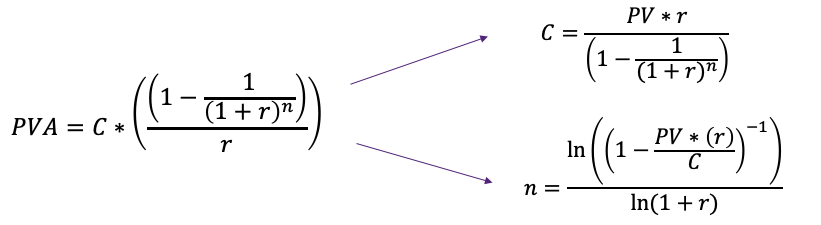
With some mathematical manipulations that are beyond the scope of this course, we can simplify this equation to yield the present value of an annuity formula:
Where:
[latex]𝐶𝐹[/latex] = level and equally spaced cash flow
[latex]𝑟[/latex]= discount rate, or interest rate
[latex]𝑛[/latex]= number of periods (often referred to as the annuity’s maturity)
Let’s apply the PVA equation to the example involving a 3-year annuity with a $1000 annual cash flow at 8%. To solve for [latex]PVA_n[/latex], we simply plug our values into the equation:
This is equal to the $2577.10 we calculated by hand earlier.
Exercises
Let’s test your knowledge
UQ Ltd is expecting annual interest income of $34,225 for the next 7 years from long term notes receivable. What is the present value of this annuity if the discount rate is 8.5%?
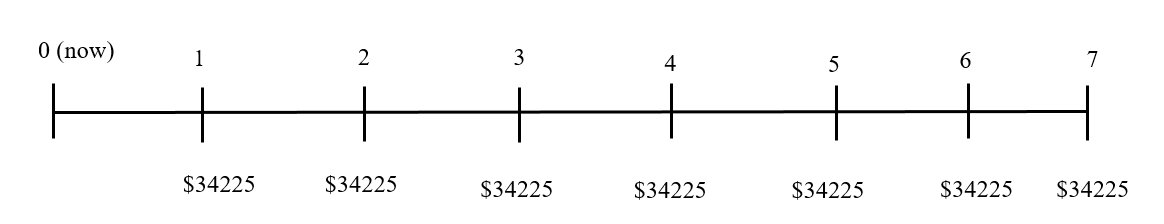
4.3.2 Re-arranging the PVA Equation
The formula for the present value of an annuity has four variables:
- Present value (PVA)
- Amount of each annuity payment (CF)
- Interest rate (r), and
- Number of annuity payments (n)
Thus, if you know three of these variables, the remaining unknown variable can be easily computed. The video below shows how to rearrange the PVA equation to solve for monthly or yearly payments (CF), interest rate (r) , and the number of payments (n).
Present Value of an Annuity (PVA):
VIDEO: Re-arranging the PVA formula (YouTube, 2m)
4.3.3 Solving for an Annuity Payment (CF)
4.3.3.1 Finding monthly or yearly payments
A very common problem in finance is determining the payment schedule for a loan on a consumer asset such as a car or a house that was purchased on credit. Nearly all consumer credit loans call for equal payments, e.g. monthly, fortnightly or weekly.
From the example, we know that the present value of the annuity is $500,000. It is the price of the apartment less the deposit made ($550,000 - $50,000), which is how much you have to borrow. We also know the number of payments - since the payments will be made monthly for 20 years, you will make 240 payments in total (12 months x 20 years).
Because the payments are made monthly, both the interest rate and maturity must be expressed in monthly terms.
This step is essential to ensure a consistent time horizon is applied throughout the computation. To get the monthly interest rate, we simply divide the annual quoted interest rate by 12. Thus, the monthly interest rate equals 0.6667% (8% / 12 months = 0.6667% per month). What we need to calculate is the monthly cash payment (CF) over the loan period.
Start by drawing a timeline to help visualise the problem:

To find monthly payments, we plug all the data into the present value of annuity formula (PVA).
[latex]CF=\frac{PVA_n\ast\ r}{\left(1-\frac{1}{\left(1+r\right)^n}\right)}[/latex]
[latex]CF=\frac{$500\ 000\ast0.006667}{1-\frac{1}{\left(1.006667\right)^{240}}}[/latex]
[latex]CF=\frac{$3\ 333.50}{0.797189}[/latex]
[latex]=$4182.20[/latex]
(Note that this is a very large monthly amount that most people would be unable to afford. The deposit put in is also less than 10% of the total value of the house. This makes it unlikely that a bank will let you take out this loan)
Exercise
Suppose that you are thinking about installing solar panels on your roof. You are looking to purchase panels at a cost of $5,000. You have been offered a loan for the entire amount of the purchase by your bank. The loan has an annual 7% interest rate, a lifespan of 5 years, and monthly repayments (12 per year). What are the monthly repayments on this loan?
4.3.4 Solving for Annuity Payment (CF) – Amortisation Schedule
4.3.4.1 Finding monthly or yearly payments using a loan amortisation schedule
Once you understand how to compute a monthly or yearly loan payment, you are ready to prepare a loan amortisation schedule. The term amortisation describes the way in which the principal (the amount borrowed) is repaid over the life of a loan. With an amortising loan, some portion of each month’s loan repayment goes to reducing the principal. When the final loan payment is made, the unpaid principal is reduced to zero and the loan is paid off. The other portion of each loan payment is interest, which is payment for the use of outstanding principal (the amount of money still owed). Thus, with an amortising loan, each loan payment contains some repayment of principal and interest payment. Nearly all loans to consumers are amortising loans.
A loan amortisation schedule is just a table that shows the loan balance at the beginning and end of each period, the payment made during that period, and how much of that payment represents interest and how much represents repayment of principal. To see how a loan amortisation schedule is prepared, consider an example as follows.
Prepare a loan amortisation schedule to show:
- What is the amount of your semi-annual repayments?
- Calculate the outstanding balance on the loan after 3 years, assuming you have made all standard repayments.
First, we calculate the loan repayment. For consumer loans, the amount of the loan payment is fixed, hence all payments are identical in amount. Therefore, we first solve for CF:
[latex]CF=\frac{PVA_n\ast\ r}{\left(1-\frac{1}{\left(1+r\right)^n}\right)}[/latex]
[latex]CF=\frac{$60\ 000\ast\frac{0.09}{2}}{\left(1-\frac{1}{\left(1+\frac{0.09}{2}\right)^{10}}\right)}[/latex]
[latex]CF=\frac{$2\ 700}{0.356072}=$7,582.73[/latex]
Hence, to answer the question (a), the amount of your semi-annual repayments is $7,582.73.
To calculate the outstanding balance on the loan after 3 years, you will need to look at a loan amortisation schedule. For the first year, the values are determined using steps as follows:
1. The amount borrowed, or the beginning principal balance is $60,000.
2. The semi-annual loan payment, as calculated earlier, is $7,582.73.
3. The interest payment for the first payment is $2,700, calculated as follows:
[latex] Interest\ payment=r\times\ P_0[/latex]
[latex]=0.09/2\times$60,000[/latex]
[latex]=$2,700[/latex]
4. The principal paid for the year is $4,882.73, calculated as follows:
[latex]Principal\ paid = Loan\ payment - Interest\ payment[/latex]
[latex]=$7,582.73−$2,700[/latex]
[latex]=$4,882.73[/latex]
5. The ending principal balance is $55,117.27, calculated as follows:
[latex]Ending\ principal\ balance = Beginning\ principal\ balance - Principal\ paid[/latex]
[latex]=$60000−$4,882.73[/latex]
[latex]=$55,117.27[/latex]
[latex]Interest\ payment =𝑟×P_0[/latex]
[latex]=0.09/2×$55,117.27[/latex]
[latex]=$2,480.28[/latex]
Putting these computations into a table gives us the entire amortisation schedule for the loan:
|
Payment No. |
Beginning Balance |
Interest Payment |
Principal Payment |
Ending Balance |
|---|---|---|---|---|
|
0 |
|
|
|
60,000.00 |
|
1 |
60,000.00 |
2,700.00 |
4,882.73 |
55,117.27 |
|
2 |
55,117.27 |
2,480.28 |
5,102.45 |
50,014.82 |
|
3 |
50,014.82 |
2,250.67 |
5,332.06 |
44,682.76 |
|
4 |
44,682.76 |
2,010.72 |
5,572.01 |
39,110.75 |
|
5 |
39,110.75 |
1,759.98 |
5,822.75 |
33,288.01 |
|
6 |
33,288.01 |
1,497.96 |
6,084.77 |
27,203.24 |
|
7 |
27,203.24 |
1,224.15 |
6,358.58 |
20,844.65 |
|
8 |
20,844.65 |
938.01 |
6,644.72 |
14,199.93 |
|
9 |
14,199.93 |
639.00 |
6,943.73 |
7,256.20 |
|
10 |
7,256.20 |
326.53 |
7,256.20 |
- |
VIDEO: Constructing an amortisation schedule in excel (YouTube, 9m10s)
Download the Excel template (XLSX, 14KB)
Download the Solution (XLSX, 15.3KB)
These calculations make sense because each loan payment includes some principal repayment. This is why the interest in column 3 declines each year. We repeat the calculations until the loan is fully amortised, at which point the principal balance goes to zero and the loan is paid off. Therefore, to answer the question (b), the outstanding balance on the loan after 3 years (6 payments) is $27,203.24.
4.3.5 Solving for Number of Annuity Payments (n) Given PVA
4.3.5.1 Finding the number of payments (n)
Another important calculation is determining the number of payments for an annuity. By re-arranging the PVA formula for n we found:
[latex]n=-\frac{ln\left(1-\frac{PV\times\ r}{CF}\right)}{\ln{\left(1+r\right)}}[/latex]
The number of payments tells us for example the time required on an annuity contract to repay a debt. Suppose you currently owe $3450 on a car loan. If you are charged 11.6% per annum, how long will it take you to pay off the loan assuming you are making $600 annual repayments.
[latex]n=-\frac{ln\left(1-\frac{PV\times\ r}{CF}\right)}{\ln{\left(1+r\right)}}[/latex]
[latex]n=-\frac{ln\left(1-\frac{$3\ 450\times0.116}{$600}\right)}{\ln{\left(1+0.116\right)}}[/latex]
[latex]n=\ -\frac{ln\ (3.003003)}{ln\ (1.116)}[/latex]
[latex]n=10\ payments[/latex]
[latex]n=10\ years[/latex]
Solving this problem as shown above, we find that it will take 10 payments for you to pay off this loan. Since you are making annual payments, this equals 10 years.
Using excel to solve for n
If you’d like to use excel, you can use the function “=nper()”, however, you must enter either pmt of pv as a negative, as excel looks at it from the perspective from one side of the transaction.
For the example above you would enter:
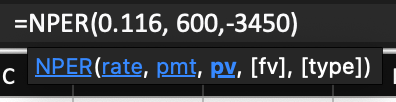
We close the bracket after our PV, because we do not have an additional payment occurring at the end of our time period (i.e. no PV). When hitting enter, you should get the same value of 10 years.
Exercise
Test your knowledge.
Your parents invested in a little studio apartment in St Lucia when you started your studies for $250,000. They paid a deposit of $50,000 and borrowed the remaining amount. They can afford to make loan repayments of $350 a week. How long will it take them to repay the loan in full? The interest rate on the loan is 2.6% per year, compounded weekly.
4.3.6 Solving for Interest Rate (r)
4.3.6.1 Finding interest rate (r)
Another important calculation is determining the interest rate, or discount rate for an annuity. The interest rate tells us the rate of return on an annuity contract. For example, suppose your parents are getting ready to retire and decide to convert some of their superannuation into an annuity that guarantees them a fixed annual income. Their superannuation fund manager asks for $350,000 for an annuity that guarantees to pay them $50,000 a year for 10 years. What is the rate of return on the annuity?
As we did in the previous section when finding annual payment, we can insert these values into PVA formula.
[latex]PVA_n=CF\times\frac{1-\frac{1}{\left(1+r\right)n}}{r}[/latex]
[latex]350,000=$50,000\times\frac{1-\frac{1}{\left(1+r\right)^{10}}}{r}[/latex]
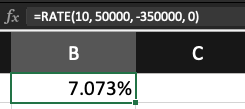
To determine the rate of return for the annuity, we need to solve the equation for the unknown value r. Unfortunately, it is not possible to solve the resulting equation for r algebraically. The only way to solve the problem manually is by trial and error. Fortunately, with the aid of technology, we can also solve this kind of problem using excel. To illustrate how to find the interest rate for an annuity using excel, the function =RATE() is used as illustrated below:
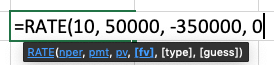
When you hit enter it will show 7.073%
Exercise
Easy Finance lets you borrow money very easily. You are looking at buying a new washing machine for $1000 and they quote you the following to borrow the $1000, to be repaid in weekly instalments over a year (52 weeks): "Only $40 a week". What is the interest rate Easy Finance charges you?
4.4 Annuities – Future Value
4.4.1 Future Value of an Annuity
Generally, when we are working with annuities, we are interested in calculating their present value. On occasion, though, we need to calculate the future value of an annuity (FVA). Such calculations typically involve some type of saving activity, such as a monthly savings plan. Another application is calculating terminal values for retirement or superannuation plans with constant contributions. We will start with a simple example:
To solve this problem, we can first lay out the cash flows on a timeline.

We can then calculate the future value for each cash flow using the future value equation [latex]FV_n=PV\times\left(1+r\right)^n[/latex]. Finally, we can add up all the cash flows. Given that the total future value of the four payments is $4506.11, you should have enough money to buy the bike.
The year 1 deposit earns interest for three years: [latex]$1000\times{(1.08)}^3=$1259.71[/latex]
The year 2 deposit earns interest for two years: [latex]$1000\times{(1.08)}^2=$1166.40[/latex]
The year 3 deposit earns interest for one year: [latex]$1000\times{(1.08)}^1=$1080.00[/latex]
The final, year 4, deposit is placed in the account at the same time as it is withdrawn, so it earns no interest: [latex]$1000\times{(1.08)}^0=$1000.00[/latex]
Adding these up, total future value = $4506.11.
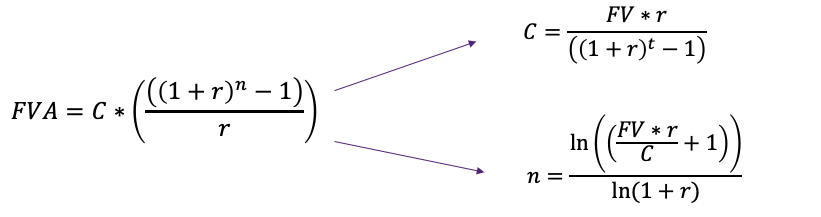
Similar to PVA, one way to simplify these computations is by using a future value of annuity formula (FVA).
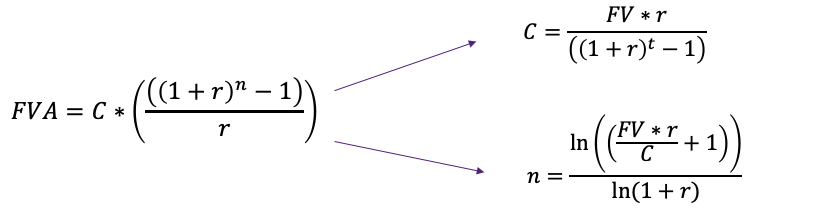
The Future Value of an Annuity formula is
Where...
[latex]FVA_n[/latex]= Future value of an annuity at the end of n periods
[latex]PVA_n[/latex] = Present value of an n period annuity
[latex]CF[/latex] = Level and equally spaced cash flow
[latex]r[/latex]= Discount rate, or interest rate
[latex]n[/latex] = Number of periods
Using the above equation to calculate FVA for the motorcycle example is straightforward. The calculation and process are similar to those we developed for PVA problems. We plug our values into the equation and yield:
[latex]FVA_n=CF\times\frac{\left(1+r\right)^n-1}{r}[/latex]
[latex]=$1000\times\frac{\left(1+0.08\right)^4-1}{0.08}[/latex]
[latex]=$1000\times4.50611[/latex]
[latex]=$4506.11[/latex]
This value is the same as the one we calculated previously using a series of future value calculations.
Exercise
Let’s test your knowledge before you go on…
You are saving up to buy a new computer, and hope to have saved $4,000 at the end of 12 months. After looking at your budget, you decide to deposit $325 per month into an account that pays 3% per year compounded monthly (0.25% per month). How much will you have in the account in 12 months?
4.4.2 Rearranging the FVA Equation
The formula for the future value of an annuity has four variables:
- Future value (FVA)
- Interest rate (r)
- Number of annuity payments (n), and
- Amount of each annuity payment (CF).
Thus, if you know three of these variables, the remaining unknown variable can be easily computed. In the following sections, we show how to rearrange the FVA equation to solve for monthly or yearly payments (CF), interest rate (r), and the number of payments (n).
Future Value of an Annuity (FVA):
Handout: Re-arranging the FVA formula (optional- click on the link below):
4.4.3 Solving for Annuity Payment (CF)
A common problem of financing is determining the value of the payments needed to achieve a certain goal at a future date. For example, saving for retirement through superannuation is usually done through a number of equal payments, e.g. $1000, over a predetermined set of time, e.g. 30 years, at a regular time-interval, e.g. annually.
To find the value of these equal payments we can use our re-arranged FVA formula for CF:
[latex]CF=\frac{FVA_n\times\ r}{\left(1+r\right)^n-1}[/latex]
Start by drawing a timeline to help visualise the problem:
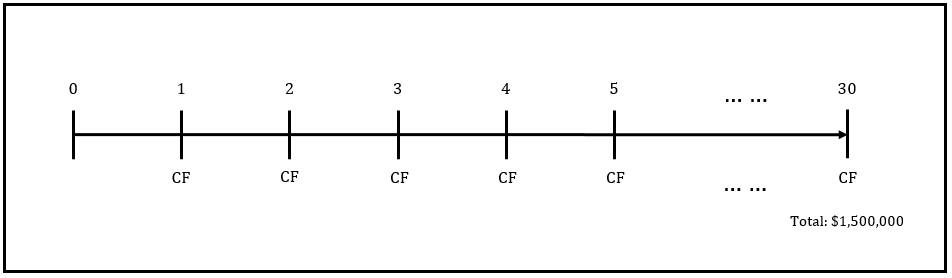
From this timeline we can see that we know all but one input (CF).
Future Value of Annuity (FVA): $1,500,000
Number of Payments (n): 30
interest-rate (r): 6%
CF: unknown.
[latex]CF=\frac{FVA_n\times\ r}{\left(1+r\right)^n-1}[/latex]
[latex]CF=\frac{1500000\times0.06}{\left(1+0.06\right)^{30}-1}[/latex]
[latex]CF=18973.36[/latex]
Test your knowledge…
Suppose that you are thinking about buying the new Tesla Truck. The truck currently retails for $60,000. Due to your poor credit rating, you have not been approved for a loan. You will have to save up for the truck over the next four years. The truck will cost $60,000 in 4 years. Your bank offers you 8% annual interest rate compounded semi-annually (4% every 6 months) for your savings account. To meet this, what will you need to save every semi-annual period for the next four years?
4.4.4 Solving FVA Equation for Interest Rate (r)
Often in many of these cases, people have i) a savings goal in mind, ii) a time-span in mind, iii) and the amount of money they can contribute to that goal each period. However, many do not consider that the interest rate has a big influence on achieving their goal. The interest rate you receive affects the CF you are required to save. Conversely, the CF you choose to save affects the rate you require to achieve a certain goal.
Let's draw a timeline.
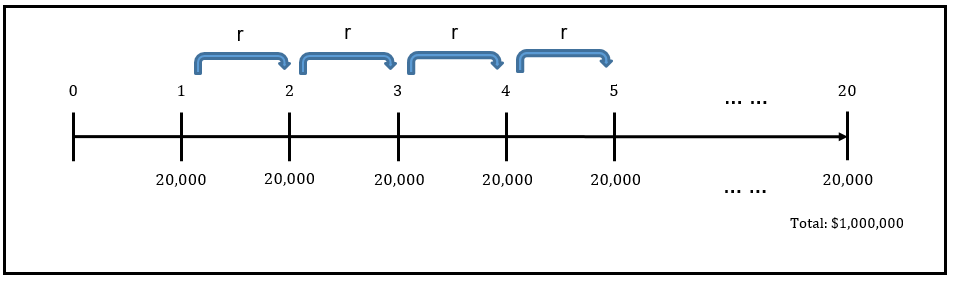
From this example, we know all but one input (interest rate).
FVA = $1,000,000
CF = $20,000
n= 20
r= unknown.
Now, let's use the FVA to solve for r.
[latex]FVA_n=CF\times\frac{\left(1+r\right)^n-1}{r}[/latex]
[latex]1000000=20000\times\frac{\left(1+r\right)^{20}-1}{r}[/latex]
However, as you may have noticed, we can not solve this equation algebraically (with pen and paper). We need to use a computer to solve for r. This can be done via i) Microsoft Excel or ii) a financial calculator.
i) Solving via Microsoft Excel:
To find the interest-rate use the 'RATE' function.
The RATE function takes in the following arguments:
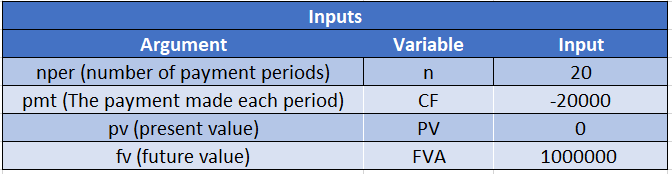
For this example we calculate '=RATE(20, -20000,0,1000000)' .The rate = 8.8%.
ii) Solving via a Financial Calculator, the steps are:

Exercise
Your employer contributes a portion of your salary to your superannuation fund every fortnight. When you retire in 40 years, you would like to have $1,000,000. Assuming the contributions to superannuation are constant at $400, what fortnightly return is required to meet your goal?
4.4.5 Solving for Number of Annuity Payments (n)
Previously we re-arranged the FVA formula to solve for n:
[latex]n=\frac{ln\left(1+\frac{FVA_n\times\ r}{CF}\right)}{ln(1+r)}[/latex]
Start by drawing a timeline to help visualise the problem:
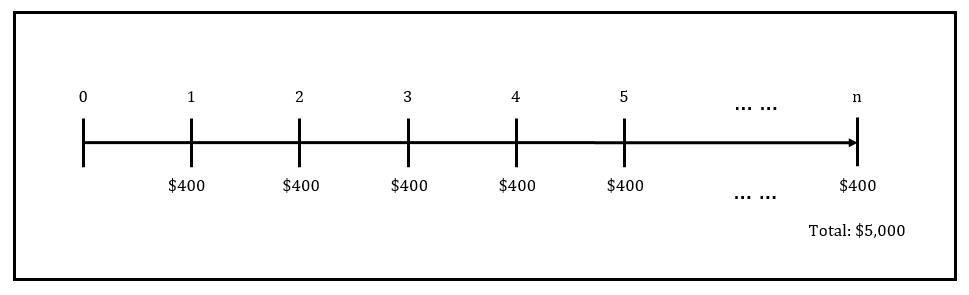
From this timeline we can see that we know all but one input (n).
FVA = $5,000
CF = $400
r = 3%
n (number of semi-annual periods) = unknown.
[latex]n=\frac{ln\left(1+\frac{FVA_n\times\ r}{CF}\right)}{\ln{\left(1+r\right)}}[/latex]
[latex]n=\frac{ln\left(1+\frac{5000\times0.03}{4000}\right)}{ln(1.03)}[/latex]
[latex]n=\frac{ln\left(1.375\right)}{ln\left(1.03\right)}[/latex]
[latex]n=10.7736[/latex]
[latex]years=\frac{10.7736}{2}=5.3867[/latex]
Or excel you enter: =NPER(0.03, 400, 0, -5000) (remember that Excel assumes you are on one side of the transaction, you either receive 400 every semi-annual and then pay 5000 at the end (the bank’s perspective) or you pay 400 every semi-annual and then receive 5000 at the end (your perspective). The answer of course will be the same.
Multiple Choice
Remember the example in the previous section: Your employer contributes a portion of your salary to your superannuation fund every fortnight. When you retire in 40 years, you would like to have $1,000,000. Assuming the contributions to superannuation are constant at $400, what fortnightly return is required to meet your goal? The answer was 0.15% per fortnight. If you expect the rate to be 0.2% per fortnight, how long will do you expect it will take you to reach your retirement goal?
4.5 Perpetuities
4.5.1 Level Cash Flows: Perpetuities
A perpetuity is a constant stream of cash flows that goes on forever. Perpetuities in the form of bonds were used by the British Treasury to pay off the debt incurred by the government to the Napoleonic wars. These perpetual bonds, called consols, have no maturity date and are still traded in the international bond markets today. They will only be retired when the British Treasury repurchases them all in the open market.
In the corporate world, perpetuities are widely used by companies to compute a value for investments with no fixed ending date, such as stocks. Payments from these investments theoretically never stop, making a perpetuity a stream of cash flows that has no end limit.
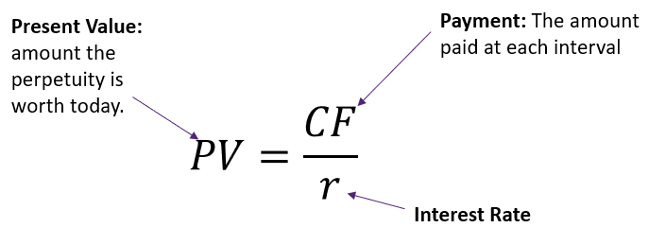
From the PVA equation, we can calculate the present value of perpetuity by setting n, which is the number of periods, equal of infinity (∞). When that is done, the value of the term 1/(1+r)∞ approaches 0,
and thus...
[latex]PVP=\frac{CF}{r}[/latex]
Where...
PVP = Present value of perpetuity
CF = Amount of constant cash flow received every period
r = Interest rate or required rate of return.
As you can see, the present value of a perpetuity is the promised constant cash payment (CF) divided by the interest rate (r). A nice feature of the equation is that it is algebraically very simple to work with since it allows us to solve for r directly rather than by trial and error.
For example, suppose you became a successful entrepreneur and decided to give back to your university by creating or endowing a scholarship fund to finance students. The goal of the fund is to provide the university with $100,000 of financial support for finance students each year forever. If the interest rate is 8%, how much money will you have to give the university to provide the desired level of support? Using the PVP equation, we find that the present value of the perpetuity is:
[latex]PVP=\frac{CF}{r}[/latex]
[latex]=\frac{100,000}{0.08}[/latex]
[latex]=$1,250,000[/latex]
Thus, a gift of $1.25 million will provide a constant annual payment of $100,000 to the university forever.
There is a subtlety that you should be aware of. In the above computations, we made no adjustment for inflation. If the economy is expected to experience inflation, which is generally the case, the real value of the scholarships you are funding will decline each year.
Before we finish our discussion of perpetuities, we should point out that the present value of a perpetuity is typically not very different from the present value of a very long annuity. For example:
Let’s test your knowledge before you go on…..
Knowledge Check
1. What is the difference between a perpetuity and an annuity?
2. Calculate the present value of a perpetuity of $1250 per year when the interest rate is 7% per annum.
4.6 Summary & Key Formulas
4.6.1 Summary
This chapter has applied the time value of money to multiple cash flows. We cannot compare cash flows occurring at different points in time, so we need to convert them to one common point in time:
- Step 1: prepare a time line to identify the magnitude and timing of the cash flows.
- Step 2: calculate the value of each cash flow as a common point in time, i.e. PV or FV.
- Step 3: add up present or future values.
If our cash flows are equal in magnitude, equally spaced, and finite, then the stream of cash flows is called annuity and we can use a short-cut formula, the annuity formula to calculate the PV or FV. Payments can be any frequency (e.g. monthly, annual). Examples of annuities are loans and retirement savings. Like the FV formula in Chapter 3, the annuity formula’s for PVA and FVA can also be re-arranged to find CF and n. Solving for r requires a financial calculator or excel. Which formula you need to use depends on the question, so always draw a timeline to make this easier! Finally, when computing present or future value of an annuity, the n is the number of payments, and r is expressed as the interest rate per period (per month for monthly payments, per year for annual payments, etc.).
If our cash flows are equal in magnitude, equally spaced and infinite, then the stream of cash flows is called a perpetuity and we can use the perpetuity formula (the easiest formula you'll learn in finance!)
We also constructed amortisation schedules to show how loans work and how our formulas work in practice.
4.6.2 Key Formulas
Present Value of an Annuity (PVA):
Future Value of an Annuity (FVA):
Perpetuity: